
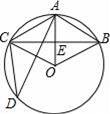
如图,在半径为6cm的⊙O中,点A是劣弧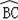
 的中点,点D是优弧
的中点,点D是优弧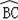
 上一点,且∠D=30°,下列四个结论:
上一点,且∠D=30°,下列四个结论:
①OA⊥BC;②BC=6
 ;③sin∠AOB=
;③sin∠AOB=
 ;④四边形ABOC是菱形.
;④四边形ABOC是菱形.
其中正确结论的序号是( )


A.①③ B.①②③④ C.②③④ D.①③④
B【考点】垂径定理;菱形的判定;圆周角定理;解直角三角形.
【专题】几何图形问题.
【分析】分别根据垂径定理、菱形的判定定理、锐角三角函数的定义对各选项进行逐一判断即可.
【解答】解:∵点A是劣弧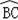
 的中点,OA过圆心,
的中点,OA过圆心,
∴OA⊥BC,故①正确;
∵∠D=30°,
∴∠ABC=∠D=30°,
∴∠AOB=60°,
∵点A是劣弧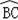
 的中点,
的中点,
∴BC=2CE,
∵OA=OB,
∴OA=OB=AB=6cm,
∴BE=AB•cos30°=6×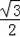
 =3
=3
 cm,
cm,
∴BC=2BE=6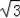
 cm,故②正确;
cm,故②正确;
∵∠AOB=60°,
∴sin∠AOB=sin60°=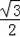
 ,
,
故③正确;
∵∠AOB=60°,
∴AB=OB,
∵点A是劣弧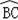
 的中点,
的中点,
∴AC=AB,
∴AB=BO=OC=CA,
∴四边形ABOC是菱形,
故④正确.
故选:B.

【点评】本题考查了垂径定理、菱形的判定、圆周角定理、解直角三角形,综合性较强,是一道好题.


科目:初中数学 来源: 题型:
矩形ABCD中,AB=4,BC=8,矩形CEFG上的点G在CD边,EF=a,CE=2a,连接BD、BF、DF,则△BDF的面积是( )


A.32 B.16 C.8 D.16+a2
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.
(1)求证:BE=CE;
(2)试判断四边形BFCD的形状,并说明理由;
(3)若BC=8,AD=10,求CD的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
图1是小明在健身器材上进行仰卧起坐锻炼时情景.图2是小明锻炼时上半身由EM位置运动到与地面垂直的EN位置时的示意图.已知BC=0.64米,AD=0.24米,α=18°.(sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
(1)求AB的长(精确到0.01米);
(2)若测得EN=0.8米,试计算小明头顶由M点运动到N点的路径弧MN的长度(结果保留π)


查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知:如图,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y=
 (x>0)经过D点,交BC的延长线于E点,且OB•AC=160,有下列四个结论:
(x>0)经过D点,交BC的延长线于E点,且OB•AC=160,有下列四个结论:
①双曲线的解析式为y=
 (x>0);②E点的坐标是(5,8);③sin∠COA=
(x>0);②E点的坐标是(5,8);③sin∠COA=
 ;④AC+OB=12
;④AC+OB=12
 .其中正确的结论有( )
.其中正确的结论有( )


A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
嘉淇想证明三角形内角和是180°和其他一些的命题.请完成下列一些命题和证明.
(1)怎样证明三角形内角和是180°呢?
(2)已知命题:等腰三角形底边上的中线和顶角的角平分线重合,证明这个命题,并写出它的逆命题,逆命题成立吗?
命题: 底边上的中线和顶角的角平分线重合的三角形是等腰三角形
证明: 证明:在△ABD和△ACD中,
∵
 ,
,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD
由此我们不难发现: 此命题是互逆命题
那么怎样证明呢?请写出证明过程.(可以画出作图痕迹.)


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com