练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若反比例函数y=的图象经过点（2，﹣1），则该反比例函数的图象在　　象限．


    二、四

    【考点】反比例函数的性质．

    【分析】用待定系数法求反比例函数的解析式，根据反比例函数的性质得出答案即可．

    【解答】解：∵反比例函数y=的图象经过点（2，﹣1），

    ∴k=﹣2，

    ∵k=﹣2＜0，

    ∴图象过二、四象限，

    故答案为：二、四．

    【点评】本题考查了反比例函数的性质，对于反比例函数y=（k≠0），（1）k＞0，反比例函数图象在第一、三象限；（2）k＜0，反比例函数图象在第二、四象限内．

    　


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    已知x、y满足方程组：，则（x+y）x﹣y的值为　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    随着人们生活质量的提高，净水器已经慢慢走入了普通百姓家庭，某电器公司销售每台进价分别为2000元、1700元的A、B两种型号的净水器，下表是近两周的销售情况：

     销售时段

     销售数量

     销售收入

     A种型号

     B种型号

     第一周

     3台

     5台

     18000元

     第二周

     4台

     10台

     31000元

    （1）求A，B两种型号的净水器的销售单价；

    （2）若电器公司准备用不多于54000元的金额在采购这两种型号的净水器共30台，求A种型号的净水器最多能采购多少台？

    （3）在（2）的条件下，公司销售完这30台净水器能否实现利润为12800元的目标？若能，请给出相应的采购方案；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    直线l的解析式是y=kx+2，其中k是不等式组的解，则直线l的图象不经过（　　）

    A．第一象限 B．第二象限  C．第三象限 D．第四象限

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在平面直角坐标系中，正方形OABC的边长为4，顶点A、C分别在x轴、y轴的正半轴，抛物线y=﹣x2+bx+c经过B、C两点，点D为抛物线的顶点，连接AC、BD、CD．

    （1）求此抛物线的解析式．

    （2）求此抛物线顶点D的坐标和四边形ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在半径为6cm的⊙O中，点A是劣弧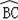的中点，点D是优弧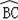上一点，且∠D=30°，下列四个结论：

    ①OA⊥BC；②BC=6；③sin∠AOB=；④四边形ABOC是菱形．

    其中正确结论的序号是（　　）

    A．①③ B．①②③④  C．②③④     D．①③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下面四个几何体中，俯视图为四边形的是（　　）

    A．  B．   C．    D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知一个圆锥的底面半径长为3cm、母线长为6cm，则圆锥的侧面积是　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图1，A、B两地在一条河的两岸，现要在河上造一座桥MN．桥造在何处才能使从A到B的路径AMNB最短？（假定河的两岸是平行的直线，桥要与河垂直）

    【问题解决】

    如图2，过点B作BB′⊥l2，且BB′等于河宽，连接AB′交l1于点M，作MN⊥l1交l2于点N，则MN就为桥所在的位置．

    【类比联想】

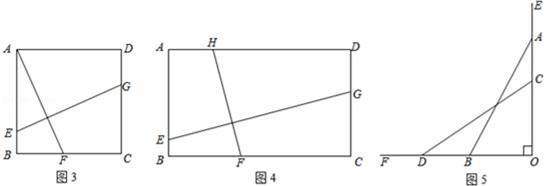
    （1）如图3，正方形ABCD中，点E、F、G分别在AB、BC、CD上，且AF⊥GE，求证：AF=EG．

    （2）如图4，矩形ABCD中，AB=2，BC=x，点E、F、G、H分别在AB、BC、CD、AD上，且EG⊥HF，设y=，试求y与x的函数关系式．

    【拓展延伸】

    如图5，一架长5米的梯子斜靠在竖直的墙面OE上，初始位置时OA=4米，由于地面OF较光滑，梯子的顶端A下滑至点C时，梯子的底端B左滑至点D，设此时AC=a米，BD=b米．

    （3）当a=　1　 米时，a=b．

    （4）当a在什么范围内时，a＜b？请说明理由．

    查看答案和解析>>

    同步练习册答案