Question

如图1，A、B两地在一条河的两岸，现要在河上造一座桥MN．桥造在何处才能使从A到B的路径AMNB最短？（假定河的两岸是平行的直线，桥要与河垂直）

【问题解决】

如图2，过点B作BB′⊥l₂，且BB′等于河宽，连接AB′交l₁于点M，作MN⊥l₁交l₂于点N，则MN就为桥所在的位置．

【类比联想】

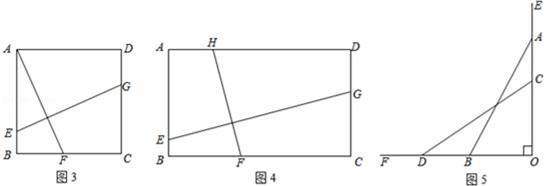
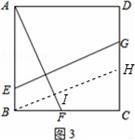
（1）如图3，正方形ABCD中，点E、F、G分别在AB、BC、CD上，且AF⊥GE，求证：AF=EG．

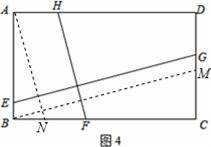
（2）如图4，矩形ABCD中，AB=2，BC=x，点E、F、G、H分别在AB、BC、CD、AD上，且EG⊥HF，设y=，试求y与x的函数关系式．

【拓展延伸】

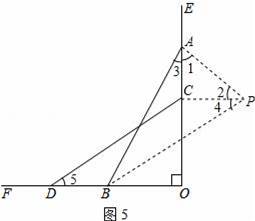
如图5，一架长5米的梯子斜靠在竖直的墙面OE上，初始位置时OA=4米，由于地面OF较光滑，梯子的顶端A下滑至点C时，梯子的底端B左滑至点D，设此时AC=a米，BD=b米．

（3）当a=　1　 米时，a=b．

（4）当a在什么范围内时，a＜b？请说明理由．

Answer 1

【考点】四边形综合题．

【分析】（1）过点作BH∥EG交CD于点H，由ASA定理得出△ABF≌△BCH，根据全等三角形的性质证明结论；

（2）作BM∥GE交CD于点M，作AN∥HF交BC于点N，根据直角三角形的性质和四边形ABCD是矩形，由相似三角形的性质得出△ABN∽△BCM，根据相似三角形的对应边成比例即可得出结论；

（3）根据勾股定理得到（4﹣a）²+（3+b）²=5²，根据a=b解方程即可；

（4）过点B作DC的平行线，过点C作OF的平行线，两线交于点P，连接AP，由题意可得DBPC为平行四边形，故可得出∠BAP=∠3+∠1=∠BPA=∠4+∠2．若a＜b，即AC＜BD=CP，因而在△ACP中，由等边对等角可知∠3＜∠5，再由锐角三角函数的定义即可得出结论．

【解答】解：（1）作BH∥EG交CD于点H．则BH=EG．

∵AF⊥EG，

∴BH⊥AF，

∴∠BIF=90°，

∴∠IBF+∠AFB=90°，

又∵直角△ABF中，∠BAF+∠AFB=90°，

∴∠BAF=∠IBF，

∴在△ABF和△BCH中，

，

∴△ABF≌△BCH，

∴AF=BH，

∴AF=EG；

（2）同理作BM∥EG交CD于点M，作AN∥HF交BC于点N．

同（1）可得∠BAN=∠MBC，

又∵∠ABN=∠C，

∴△ABN∽△BCM，

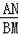
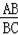
∴==，又HF=AN，EG=BM，

∴y=；

（3）解：∵CO=4﹣a，DO=3+b．

∴Rt△DOC中，DC²=（4﹣a）²+（3+b）²，

即（4﹣a）²+（3+b）²=5²．

当a=b时，有（4﹣a）²+（3+a）²=25，

解得a=1或a=0（不合）．

故答案为：1；

（4）当0＜a＜1时，a＜b．理由如下：

如图5，过点B作DC的平行线，过点C作OF的平行线，两线交于点P，连接AP．

∵CD∥BP，PC∥OF，

∴DBPC为平行四边形，

∴BP=DC，CP=BD．

又AB=DC，

∴BP=AB．

∴∠BAP=∠3+∠1=∠BPA=∠4+∠2．

若a＜b，即AC＜BD=CP，因而在△ACP中，

∵∠1＞∠2，

∴∠3＜∠4．

又∵∠5=∠4，

∴∠3＜∠5．

∵Rt△ABO中，sin∠3==，

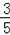
同理sin∠5==，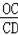

∴＞，

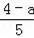
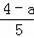
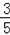
解得，0＜a＜1．

【点评】本题考查的是四边形综合题，掌握平行四边形的判定与性质、全等三角形的判定与性质、勾股定理的应用以及一元二次方程的解法是解题的关键，解答时注意锐角三角函数的定义的应用．