
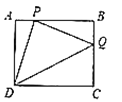
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别为直线
分别为直线![]() 、
、![]() 上的动点,且
上的动点,且![]() ,当
,当![]() 为等腰三角形时,则
为等腰三角形时,则![]() 的长为______.
的长为______.
【答案】1或7
【解析】
当P点在AB上,如图1,先根据等角的余角相等得到∠ADP=∠BPQ,则可证明Rt△ADP∽Rt△BPQ,利用相似比得到![]() =1,则PB=AD=3,然后计算AB-PB即可.当P点在AB的延长线上时,如图2,同样方法得到Rt△ADP∽Rt△BPQ,利用相似比得到PB=AD=3,然后计算AB+PB即可.
=1,则PB=AD=3,然后计算AB-PB即可.当P点在AB的延长线上时,如图2,同样方法得到Rt△ADP∽Rt△BPQ,利用相似比得到PB=AD=3,然后计算AB+PB即可.
解:当P点在边AB上,如图1,
∵四边形ABCD为矩形,
∴AD=BC=3,∠A=∠B=90°,
∵PD⊥PQ,
∴∠DPQ=90°,
∵∠APD+∠ADP=90°,∠APD+∠BPQ=90°,
∴∠ADP=∠BPQ,
∴Rt△ADP∽Rt△BPQ,
∴![]() ,
,
∴PB=AD=3,
∴AP=AB-PB=4-3=1.
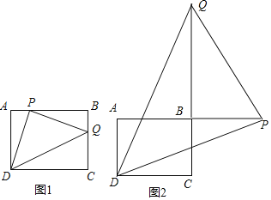
当P点在AB的延长线上时,如图2,
同样方法得到Rt△ADP∽Rt△BPQ,
∴![]() =1,
=1,
∴PB=AD=3,
∴AP=AB+PB=4+3=7.
综上所述,AP的长度为1或7.
故答案为1或7.
故答案为1或7.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=![]() (x>0)的图象与BC边交于点E.
(x>0)的图象与BC边交于点E.
(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车销售公司11月份销售某厂家的汽车,在一定范围内,每部汽车的进价与销售量有如下关系:若当月仅售出![]() 部汽车,则该部汽车的进价为
部汽车,则该部汽车的进价为![]() 万元,每多售出
万元,每多售出![]() 部,所有售出的汽车的进价均降低
部,所有售出的汽车的进价均降低![]() 万元/部.月底厂家再根据销售量返利给销售公司:销售量在
万元/部.月底厂家再根据销售量返利给销售公司:销售量在![]() 部以内(含
部以内(含![]() 部),每部返利
部),每部返利![]() 万元;销售量在
万元;销售量在![]() 部以上,每部返利
部以上,每部返利![]() 万元.
万元.
(1)若该公司当月售出![]() 部汽车,则每部汽车的进价为 万元;
部汽车,则每部汽车的进价为 万元;
(2)若汽车的售价为![]() 万元/部,该公司计划当月盈利
万元/部,该公司计划当月盈利![]() 万元,则需售出多少部汽车? (盈利=销售利润+返利)
万元,则需售出多少部汽车? (盈利=销售利润+返利)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表:
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | m | 5 | 2 | 1 | 2 | … |
则m的值是_____,当y<5时,x的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一场篮球比赛中,一名球员在关键时刻投出一球,已知球出手时离地面高2米,与篮圈中心的水平距离为7米,当球出手后水平距离为4米时到达最大高度4米,已知篮球运行的轨迹为抛物线,篮圈中心距离地面3.19米.
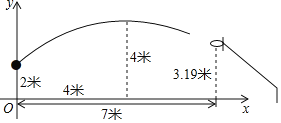
(1)以地面为x轴,篮球出手时垂直地面所在直线为y轴建立平面直角坐标系,求篮球运行的抛物线轨迹的解析式;
(2)通过计算,判断这个球员能否投中?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)已知:![]() ABCD的两边AB,AD的长是关于x的方程
ABCD的两边AB,AD的长是关于x的方程![]() 的两个实数根.
的两个实数根.
(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么![]() ABCD的周长是多少?
ABCD的周长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形网格中建立平面直角坐标系,已知△ABC三个顶点分别为A(﹣1,2)、B(2,1)、C(4,5).
(1)画出△ABC关于x对称的△A1B1C1;
(2)以原点O为位似中心,在x轴的上方画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2,并求出△A2B2C2的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,AC=6,BC=8,D边BC上的任意一点,将∠C沿过点D的直线折叠,使点C落在斜边AB上的点E处,当△BDE是直角三角形时,CD的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com