Question

9．如图，⊙P在第一象限，半径为3，动点A沿着⊙P运动一周，在点A运动的同时，作点A关于原点O的对称点B，再以AB为底边作等腰三角形△ABC，点C在第二象限，且sinA=0.8，点C随点A运动所形成的图形的面积为16π．

Answer 1

分析 如图所示，点C随A运动所形成的图形为圆，根据等腰三角形的性质求出CC′的长，即为圆的直径，求出圆的面积即可．

解答 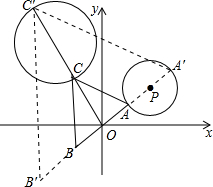解：如图所示，点C随A运动所形成的图形为圆，∵CA=CB，点A关于原点O的对称点B，
∴OC⊥AB，OA=OB，∵sinA=0.8，可得OC=$\frac{4}{3}$OA，OC′=$\frac{4}{3}$OA′，
∴CC′=OC′-OC=$\frac{4}{3}$（OA′-OA）=$\frac{4}{3}$AA′=6×$\frac{4}{3}$=8，
∴点C随点A运动所形成的圆的面积为π×4²=16π．
故答案为：16π．

点评 此题考查了轨迹，以及等边三角形的性质，根据题意得出点C随A运动所形成的图形为圆是解本题的关键．