Question

1．如图：已知反比例函数y=$\frac{{k}_{1}}{x}$与一次函数y=k₂x+b的图象交于A（2，-1），B（$-\frac{1}{2}，m$）．
（1）求k₁、k₂，b的值；
（2）求三角形AOB的面积；
（3）若M（x₁，y₁），N（x₂，y₂）是反比例函数y=$\frac{{k}_{1}}{x}$图象上的两点，且x₁＜x₂，y₁＞y₂，指出M、N各位于哪个象限，并简单说明理由．

Answer 1

分析 （1）先把A点坐标代入y=$\frac{{k}_{1}}{x}$可求出k₁=-2，则反比例函数的解析式为y=-$\frac{2}{x}$，再把B（$-\frac{1}{2}，m$）代入反比例函数解析式求出m，得到B点坐标，然后利用待定系数法求一次函数解析式即可；
（2）如图，设直线AB交y轴于C点，则C（0，3），然后根据三角形面积公式，利用S_△AOB=S_△AOC+S_△BOC进行计算；
（3）根据反比例函数的性质，在每一象限内y随x的增大而增大，而x₁＜x₂，y₁＞y₂，于是可判断M点和N点不在同一象限，则易得点M在第二象限，点N在第四象限．

解答 解：（1）把A（2，-1）代入y=$\frac{{k}_{1}}{x}$得k₁=2×（-1）=-2，
则反比例函数的解析式为y=-$\frac{2}{x}$
把B（$-\frac{1}{2}，m$）代入y=-$\frac{2}{x}$得-$\frac{1}{2}$m=-2，解得m=4，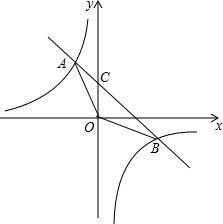
把A（2，-1）、B（-$\frac{1}{2}$，4）代入y=k₂x+b得$\left\{\begin{array}{l}{2{k}_{2}+b=-1}\\{-\frac{1}{2}{k}_{2}+b=4}\end{array}\right.$，解得$\left\{\begin{array}{l}{{k}_{2}=-2}\\{b=3}\end{array}\right.$，
则直线解析式为y=-2x+3，
即k₁、k₂，b的值分别为-2，-2，3；
（2）如图，设直线AB交y轴于C点，
当x=0时，y=-2x+3=3，则C（0，3），
所以S_△AOB=S_△AOC+S_△BOC=$\frac{1}{2}$×3×$\frac{1}{2}$+$\frac{1}{2}$×3×2=$\frac{15}{4}$；
（3）因为M（x₁，y₁），N（x₂，y₂）是反比例函数y=-$\frac{2}{x}$图象上的两点，且x₁＜x₂，y₁＞y₂，
所以M点和N点不在同一象限，其中点M在第二象限，点N在第四象限．

点评 本题考查了反比例函数与一次函数的交点问题：求反比例函数与一次函数的交点坐标，把两个函数关系式联立成方程组求解，若方程组有解则两者有交点，方程组无解，则两者无交点．也考查了反比例函数的性质．