
分析 (1)根据二次函数的定义求出m的值即可解决问题.
(2)运用当二次项系数小于0时,抛物线开口向下;
(3)运用当二次项系数大于0时,抛物线开口向上,图象有最低点,函数有最小值;
(4)根据二次函数的性质解答即可.
解答 解:(1)∵函数y=(m+3)${x}^{{m}^{2}+3m-2}$是关于x的二次函数,
∴m2+3m-2=2,m+3≠0,
解得:m1=-4,m2=1;
(2)∵函数图象的开口向下,
∴m+3<0,
∴m<-3,
∴当m=-4时,该函数图象的开口向下;
(3)∵m=-4或1,
∵当m+3>0时,抛物线有最低点,函数有最小值,
∴m>-3,
∵m=-4或1,
∴当m=1时,该函数有最小值.
(4)当m=1时,x>0时,y随x的增大而增大,x<0时,y随x的增大而减小;
当m=-4时,x>0时,y随x的增大而减小,x<0时,y随x的增大而增大.
点评 该题主要考查了二次函数的定义及其性质的应用问题;牢固掌握定义及其性质是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
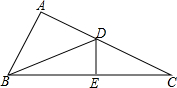 如图所示,△ADB≌△EDB,△BDE≌△CDE,点B,E,C三点在同一直线上,
如图所示,△ADB≌△EDB,△BDE≌△CDE,点B,E,C三点在同一直线上,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com