
����Ŀ��Ϊ�ƹ�������������μ䡱�������ij��ѧ������ѧ���п���A��ʵ����B��������Զ��C��������D���ܲ����ֻ��Ŀ��Ϊ���˽�ѧ����������Ŀ��ϲ������������ȡ�˲���ѧ�����е��飬�������������Ƴ���ͼ�٢ڵ�ͳ��ͼ������ͼ�е���Ϣ����������⣺ 
��1������������У��������˶�����ѧ����
��2������㱾�������ϲ����������Զ����ѧ����������ռ�ٷֱȣ���������ͳ��ͼ����������
��3�������鵽ϲ������������5��ѧ������3��������2��Ů�����ִ���5��ѧ���������ȡ2��ѧ�������û���״ͼ���б��ķ���������պó鵽ͬ�Ա�ѧ���ĸ��ʣ�
���𰸡�
��1���⣺��������ã�
15��10%=150��������
������������У���������150��ѧ����
��2���⣺���������ϲ����������Զ����ѧ�������ǣ�150��15��60��30=45���ˣ���
��ռ�ٷֱ��ǣ� ![]() ��100%=30%��
��100%=30%��
��ͼ���£�

��3���⣺��A��ʾ������B��ʾŮ������ͼ���£�

����20�������ͬ�Ա�ѧ���������8�֣�
��պó鵽ͬ�Ա�ѧ���ĸ����� ![]() =
= ![]() ��
��
����������1����A������������ռ�İٷֱȣ�������������ѧ��������2���ó�����������ȥA��C��D�����������ϲ����������Զ����ѧ���������ٳ��Ա������ѧ�����������ռ�İٷֱȣ��ٻ�ͼ���ɣ���3����A��ʾ������B��ʾŮ������������ͼ���ٸ��ݸ��ʹ�ʽ���м��㼴�ɣ�


 ��ʦ����ָ���ο�ʱϵ�д�
��ʦ����ָ���ο�ʱϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����1+��2=180�㣬��DAE=��BCF��DAƽ����BDF��
��1��AE��FC��ƽ����?˵��������
��2��AD��BC��λ�ù�ϵ���?Ϊʲô?
��3��BCƽ����DBE��?Ϊʲô��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC����AP��ֱ��ABC��ƽ����BP�ڵ�P������ABC�����Ϊ32cm2��BP=6cm,����APB���������APC�������3������AP��________cm.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�������A1B1C1D1��D1 E1E2B2��A2B2 C2D2��D2E3E4B3������ͼ��ʾ�ķ�ʽ���ã����е�B1��y���ϣ���C1��E1��E2��C2��E3��E4��C3����x���ϣ���֪������A1B1C1D1�ı߳�Ϊl����B1C1O=60�㣬B1C1��B2C2��B3C3������������A2017B2017C2017 D2017�ı߳��ǣ� �� 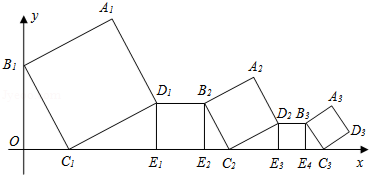
A.�� ![]() ��2016
��2016
B.�� ![]() ��2017
��2017
C.�� ![]() ��2016
��2016
D.�� ![]() ��2017
��2017
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ڡ�ABC����AB=AC����D��BC���е㣬��E��AD�ϣ�����BE��CE.
(1)��֤��BE=CE
(2)��ͼ2����BE���ӳ��߽�AC�ڵ�F����BF ��AC������ΪF��ԭ���������������䣮��֤����CAD=��CBF
(3)��(2)�������£�����BAC=45![]() ���жϡ�CFE����״����˵�����ɣ�
���жϡ�CFE����״����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������˾Ϊ���������Լ�õ磬��ȡ�����õ����ֶ��շѰ취����ij������ÿ��Ӧ�����y��Ԫ�����õ���x���ȣ��ĺ���ͼ����һ�����ߣ���ͼ��ʾ��������ͼ����������⣺
(1) �ֱ�д����0��x��100��x��100ʱ��y��x�ĺ�����ϵʽ
(2) ���ú�����ϵʽ��˵��������˾��ȡ���շѱ�
(3) �����û�ij���õ�62�ȣ���Ӧ�ɷѶ���Ԫ�������û�ij�½ɷ�105Ԫʱ������û��������˶��ٶȵ磿

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����D��E�ֱ���AB��AC�ϣ�DE��BC��F��AD��һ�㣬FE���ӳ��߽�BC���ӳ����ڵ�G.��֤��
(1)��EGH>��ADE��
(2)��EGH����ADE����A����AEF.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������Ϻ�����⡣
��ĸ�к���δ֪���IJ���ʽ�з�ʽ����ʽ���磺![]() ��
��![]() �ȡ���ô���������ǵĽ⼯�أ�
�ȡ���ô���������ǵĽ⼯�أ�
��������ѧ�������������������֪�����������ͬ�ŵ�������ŵø�������ĸ����ʽΪ��
��1����![]() ��
��![]() ����
����![]() ����
����![]() ��
��![]() ����
����![]() ��
��
��2����![]() ��
��![]() ����
����![]() ����
����![]() ��
��![]() ����
����![]() .
.
�����������⣺
��1����֮������![]() ��
��![]() ��
��![]() ������
������![]() ����__________��
����__________��
��2�������������ɣ���ʽ![]() �Ľ⼯.
�Ľ⼯.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲����е�ʽ��
12��231=132��21�� 14��451=154��41�� 32��253=352��23�� 34��473=374��43��45��594=495��54������
����ÿ����ʽ�����������Ƿֱ�ԳƵģ���ÿ����ʽ�������λ������λ��������֮�������ͬ���ɣ����dz������ʽΪ�����ֶԳƵ�ʽ����
��1������������ʽ��ӳ�Ĺ�����գ�ʹʽ�ӳ�Ϊ�����ֶԳƵ�ʽ����
��35���� ��=�� ����53�� ���� ����682=286���� ����
��2�������ֶԳ�ʽ��ߵ���λ����ʮλ����Ϊm����λ����Ϊn����2��m+n��9���ú�m��n�Ĵ���ʽ��ʾ���ֶԳ�ʽ��ߵ���λ������λ���ij˻�P�������P �ܱ�110����ʱmn��ֵ��(���г˷���ʽ![]() ����
����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com