
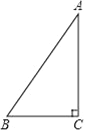
【题目】如图,在△ABC 中,∠C=90°
(1)利用尺规作∠B 的角平分线交AC于D,以BD为直径作⊙O交AB于E(保留作图痕迹,不写作法);
(2)综合应用:在(1)的条件下,连接DE
①求证:CD=DE;
②若sinA=![]() ,AC=6,求AD.
,AC=6,求AD.
【答案】(1)作图见解析;(2)①证明见解析;②AD=![]() .
.
【解析】试题分析:(1)利用角平分线的作法得出∠B的角平分线BD,根据线段垂直平分线的作法作出线段BD的垂直平分线,交BD于点O,以O为圆心,以OB长为半径作圆即可;(2)根据直径所对的圆周角为直角可得∠BED=90°,再由角平分线的性质可得CD=DE;在Rt△ADE中,sinA=![]() =
=![]() ,设DC=DE=3x,AD=5x,根据AC=AD+DC列出方程求得x的值,即可求得AD的长.
,设DC=DE=3x,AD=5x,根据AC=AD+DC列出方程求得x的值,即可求得AD的长.
试题解析:
(1)

(2)∵BD为![]() O的直径
O的直径
∴∠BED=90°,又∵∠C=90°
∴DE⊥AB,DC⊥BC
又∵BD平分∠ABC
∴DE=DC
(3)
在Rt△ADE中,sinA=![]()
∵sinA=![]()
∴![]() =
=![]()
设DC=DE=3![]() ,AD=5
,AD=5![]()
∵AC=AD+DC
∴3![]() +5
+5![]() =6
=6
![]() =
=![]()
AD=5![]() =5×
=5×![]() =
=![]()


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:
【题目】如图在给定的一张平行四边形纸片上作一个菱形,甲、乙两人的作法如下: 甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠BAD,∠ABC的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法请分别做出判断,并证明.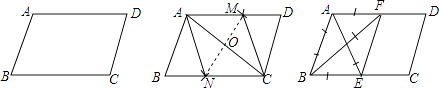
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】记M(1)=﹣2,M(2)=(﹣2)×(﹣2),M(3)=(﹣2)×(﹣2)×(﹣2),…,M(n)= ![]()
(1)填空:M(5)= , M(50) 是一个数(填“正”或“负”)
(2)计算:①2M(6)+M(7);②4M(7)+2M(8);
(3)直接写出2016M(n)+1008M(n+1)的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要使方程(a﹣3)x2+(b+1)x+c=0是关于x的一元二次方程,则( )
A.a≠0
B.a≠3
C.a≠1且b≠﹣1
D.a≠3且b≠﹣1且c≠0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有A,B,C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( ) 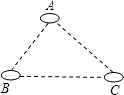
A.在AC,BC两边高线的交点处
B.在AC,BC两边中线的交点处
C.在AC,BC两边垂直平分线的交点处
D.在∠A,∠B两内角平分线的交点处
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABE向右平移2cm得到△DCF,如果△ABE的周长是16cm,那么四边形ABFD的周长是( )
A.16cm
B.18cm
C.20cm
D.21cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com