
【题目】如图,在△ABC中,AD是高,在线段DC上取一点E,使DE=BD,已知AB+BD=DC. 求证:E点在线段AC的垂直平分线上.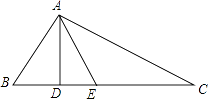
【答案】证明:∵AD是高,∴AD⊥BC, 又∵BD=DE,
∴AD所在的直线是线段BE的垂直平分线,
∴AB=AE,
∴AB+BD=AE+DE,
又∵AB+BD=DC,
∴DC=AE+DE,
∴DE+EC=AE+DE
∴EC=AE,
∴点E在线段AC的垂直平分线上
【解析】根据线段的垂直平分线性质求出BD=DE,推出DE+EC=AE+DE,得出EC=AE,根据线段垂直平分线性质推出即可.
【考点精析】本题主要考查了线段垂直平分线的性质的相关知识点,需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等才能正确解答此题.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】为鼓励同学们积极参加体育锻炼,学校计划拿出不超过2400元的资金购买一批篮球和排球,已知篮球和排球的单价比为5:1,单价和为90元.
(1)篮球和排球的单价分别是多少元?
(2)若要求购买的篮球和排球共40个,且购买的篮球数量多于28个,有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实“优化税收营商环境,助力经济发展和民生改善”的政策,国家税务总局统计数据显示,2018年5至10月合计减税2980亿元,将2980亿元用科学记数法表示为_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
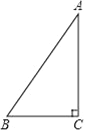
【题目】如图,在△ABC 中,∠C=90°
(1)利用尺规作∠B 的角平分线交AC于D,以BD为直径作⊙O交AB于E(保留作图痕迹,不写作法);
(2)综合应用:在(1)的条件下,连接DE
①求证:CD=DE;
②若sinA=![]() ,AC=6,求AD.
,AC=6,求AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;
②方程![]() 的两个根是x1=﹣1,x2=3;
的两个根是x1=﹣1,x2=3;
③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种正方形合金板材的成本y(元)与它的面积成正比,设边长为xcm.当x=3时,y=18,那么当成本为72元时,边长为( )
A. 6cmB. 12cmC. 24cmD. 36cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下文,寻找规律.
计算:(1﹣x)(1+x)=1﹣x2 , (1﹣x)(1+x+x2)=1﹣x3 , (1﹣x)(1+x+x2+x3)=1﹣x4….
(1)观察上式,并猜想:(1﹣x)(1+x+x2+…+xn)= .
(2)根据你的猜想,计算:1+3+32+33…+3n= . (其中n是正整数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com