
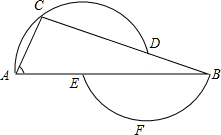
 如图,过D、A、C三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,如果∠A=66°,那么∠B=
如图,过D、A、C三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,如果∠A=66°,那么∠B=| 1 |
| 2 |
| 1 |
| 2 |
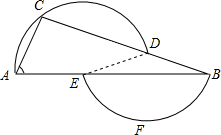 解:连接DE,
解:连接DE,| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
| 星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:
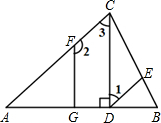 已知:在△ABC中,CD是AB边上的高,∠DEB=∠ACB,∠1+∠2=180°.试判断FG与AB的位置关系,并说明理由.请在下划线内补全解题过程或依据.
已知:在△ABC中,CD是AB边上的高,∠DEB=∠ACB,∠1+∠2=180°.试判断FG与AB的位置关系,并说明理由.请在下划线内补全解题过程或依据.查看答案和解析>>
科目:初中数学 来源: 题型:
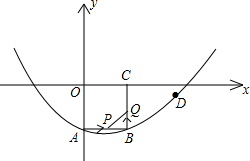 如图,在平面直角坐标系xOy中,正方形OABC的边长为2cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B和D(4,-
如图,在平面直角坐标系xOy中,正方形OABC的边长为2cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B和D(4,-| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、(x-1)(x+1)=x2-1 |
| B、(a+b)2=a2+2ab+b2 |
| C、x2-x-2=(x+1)(x-2) |
| D、ax-ay-1=a(x-y)-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com