
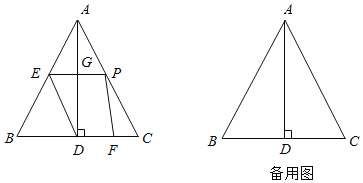
【题目】已知:如图,在等边△ABC中,AB=6cm,AD⊥BC于点D,动点F从点C出发,沿CB方向以1cm/s的速度向点D运动;同时,动点P也从点C出发,沿CA方向以3cm/s的速度向点A运动,过点P作PE∥BC,与边AB交于点E,与AD交于点G,连结ED,PF.设运动的时间为t(s)(0<t<2).
(1)当t为何值时,四边形EDFP为平行四边形?
(2)设四边形EDFP面积为y,求y与t之间的函数关系式;
(3)连结PD、EF,当t为何值时,PD⊥EF?
【答案】(1)![]() s;(2)y=﹣3
s;(2)y=﹣3![]() t2+
t2+![]() t;(3)当t=
t;(3)当t=![]() s时,PD⊥EF.
s时,PD⊥EF.
【解析】
(1)根据已知条件可推出△APE是等边三角形,由题意可得CP=3t,CF=t,则AP=6﹣3t,PE=6﹣3t,DF=DC﹣CF=3﹣t,根据四边形EDFP为平行四边形,列出方程求解即可得出答案;
(2)过点P作PH⊥BC于H,根据现有条件得出PH=![]() t,再根据y=S△ABC﹣S△APE﹣S△PCF﹣S△EDB即可得出解析式;
t,再根据y=S△ABC﹣S△APE﹣S△PCF﹣S△EDB即可得出解析式;
(3)设PD交EF于点O,过点E作EH⊥BC于H,根据已知条件推出PG=EG=![]() PE=
PE=![]() (6﹣3t),同(2)得:EH=
(6﹣3t),同(2)得:EH=![]() t,BH=
t,BH=![]() t,推出∠PDG=∠OFD,即tan∠PDG=tan∠OFD=
t,推出∠PDG=∠OFD,即tan∠PDG=tan∠OFD=![]() =
=![]() ,据此列式求解即可.
,据此列式求解即可.
解:(1)∵等边△ABC中,AB=6cm,AD⊥BC,
∴AC=AB=BC=6,DC=BD=![]() BC=3,∠B=∠C=60°,
BC=3,∠B=∠C=60°,
∵PE∥BC,
∴∠APE=∠AEP=∠B=∠C=60°,
∴△APE是等边三角形,
∴AP=PE,
由题意得:CP=3t,CF=t,则AP=6﹣3t,
∴PE=6﹣3t,DF=DC﹣CF=3﹣t,
∵四边形EDFP为平行四边形,
∴PE=DF,
∴6﹣3t=3﹣t,
∴t=![]() ,
,
∴当t=![]() s时,四边形EDFP为平行四边形;
s时,四边形EDFP为平行四边形;
(2)过点P作PH⊥BC于H,如图1所示:
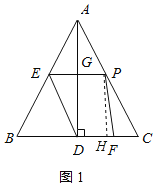
由勾股定理得:AD=![]() =
=![]() =3
=3![]() ,
,
∵∠C=60°,
∴sin60°=![]() =
=![]() ,
,
∴PH=![]() ×3t=
×3t=![]() t,
t,
∵PE∥BC,AD⊥BC,PH⊥BC,
∴四边形PGDH是矩形,
∴PH=DG,
∴y=S△ABC﹣S△APE﹣S△PCF﹣S△EDB
=![]() ADBC﹣
ADBC﹣![]() (AD﹣PH)PE﹣
(AD﹣PH)PE﹣![]() PHCF﹣
PHCF﹣![]() PHBD
PHBD
=![]() ×3
×3![]() ×6﹣
×6﹣![]() ×(3
×(3![]() t)×(6﹣3t)﹣
t)×(6﹣3t)﹣![]() ×
×![]() t×t﹣
t×t﹣![]() ×
×![]() t×3
t×3
=﹣3![]() t2+
t2+![]() t;
t;
(3)设PD交EF于点O,过点E作EH⊥BC于H,如图2所示:

则四边形EHDG是矩形,
∴EH=DG,
∵△APE是等边三角形,
∴PG=EG=![]() PE=
PE=![]() (6﹣3t),
(6﹣3t),
同(2)得:EH=![]() t,BH=
t,BH=![]() t,
t,
∵PD⊥EF,
∴∠FOD=90°,
∴∠OFD+∠ODF=90°,
∵∠ODF+∠PDG=90°,
∴∠PDG=∠OFD,
∴tan∠PDG=tan∠OFD=![]() =
=![]() ,
,
∴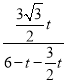 =
=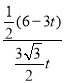 ,
,
∴2t2+11t﹣12=0,
解得:t1=![]() ,t2=
,t2=![]() (不合题意舍去),
(不合题意舍去),
则当t=![]() s时,PD⊥EF.
s时,PD⊥EF.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】为了解我市某中学“书香校园”的建设情况,在该校随机抽取了50名学生,调查了解他们一周阅读课外书籍的时间,并将调查结果绘制成如图所示的频数分布直方图(每小组的时间包含最小值,不包含最大值),根据图中信息估计该校1500名学生中,一周课外阅读时间不少于4小时的人数约为( )

A.300B.600C.900D.1200
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形的周长为60.
(1)当该矩形的面积为200时,求它的边长;
(2)请表示出这个矩形的面积与其一边长的关系,并求出当矩形面积取得最大值时,矩形的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了做好新冠肺炎疫情期间开学工作,我区某中学用药熏消毒法对教室进行消毒.已知一瓶药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例;药物释放完毕后,y与x成反比例,如图所示.根据图中提供的信息,解答下列问题:
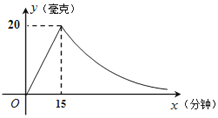
(1)写出倾倒一瓶药物后,从药物释放开始,y与x之间的两个函数关系式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量不低于8毫克时,消毒有效,那么倾倒一瓶药物后,从药物释放开始,有效消毒时间是多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明与小亮玩游戏,如图,两组相同的纸牌,每组三张,牌面数字分别是3,4,5.他们将卡片背面朝上,分组充分洗匀后,从每组纸牌中各摸出一张,称为一次游戏.当摸出的两张纸牌的牌面数字之和大于8,则小明获胜;当摸出的两张纸牌的牌面数字之和小于8,则小亮获胜.
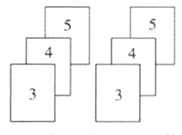
(1)请你用列表法或画树状图法求出小明获胜的概率;
(2)这个游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11·湖州)(本小题10分)
如图,已知E、F分别是□ABCD的边BC、AD上的点,且BE=DF。
⑴求证:四边形AECF是平行四边形;
⑵若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
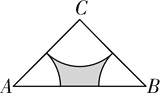
【题目】(2011贵州安顺)如图,在Rt△ABC中,∠C=90°,CA=CB=4,分别以A、B、C为圆心,以![]() AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是 .
AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某区初中学生对网络游戏的喜好和作业量多少情况,随机抽取了该区500名同学进行了调查,并将调查的情况进行了整理,如下表:
作业量多少 网络游戏的喜好 | 认为作业多 | 认为作业不多 | 合计 |
喜欢网络游戏 | 180 | 90 | 270 |
不喜欢网络游戏 | 80 | 150 | 230 |
根据抽样调查结果,估计该区12000名初中生“不喜欢网络游戏并认为作业不多”的人数是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com