
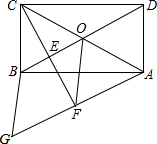
 如图,在矩形ABCD中,AC、BD相交于点O,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BO,连接BG、DF.若AG=13,CF=6,求四边形BOFG的周长.
如图,在矩形ABCD中,AC、BD相交于点O,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BO,连接BG、DF.若AG=13,CF=6,求四边形BOFG的周长.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 41 |
| 3 |


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
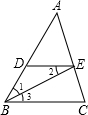 请把下列说理过程补充完整:
请把下列说理过程补充完整:查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 2 |
| 25 |
| 64 |
查看答案和解析>>
科目:初中数学 来源: 题型:
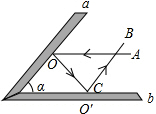 如图,两个平面镜a、b的夹角为α,平行于b的光线AO入射到α上,经过两次反射后的反射光线0’B平行于a,则角α等于( )
如图,两个平面镜a、b的夹角为α,平行于b的光线AO入射到α上,经过两次反射后的反射光线0’B平行于a,则角α等于( )| A、70° | B、60° |
| C、45° | D、30° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com