
【题目】如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(﹣4,0),B(0,3),动点P从点O出发,沿x轴负方向以每秒1个单位的速度运动,同时动点Q从点B出发,沿射线BO方向以每秒2个单位的速度运动,过点P作PC⊥AB于点C,连接PQ,CQ,以PQ,CQ为邻边构造平行四边形PQCD,设点P运动的时间为t秒. 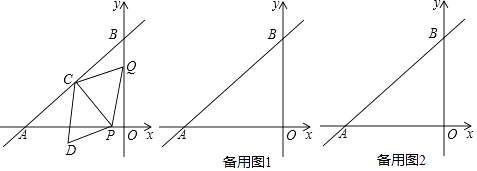
(1)当点Q在线段OB上时,用含t的代数式表示PC,AC的长;
(2)在运动过程中. ①当点D落在x轴上时,求出满足条件的t的值;
②若点D落在△ABO内部(不包括边界)时,直接写出t的取值范围;
(3)作点Q关于x轴的对称点Q′,连接CQ′,在运动过程中,是否存在某时刻使过A,P,C三点的圆与△CQQ′三边中的一条边相切?若存在,请求出t的值;若不存在,请说明理由.#D.
【答案】
(1)解:如图1中,
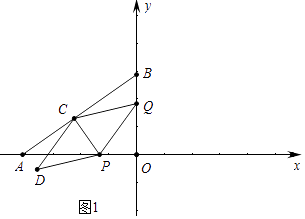
∵OA=3,OB=4,
∴AB= ![]() =
= ![]() =5,
=5,
在Rt△ACP中,PA=4﹣t,
∵sin∠OAB= ![]() =
= ![]() ,
,
∴PC= ![]() (4﹣t),
(4﹣t),
∵cos∠OAB= ![]() =
= ![]() ,
,
∴AC= ![]() (4﹣t)
(4﹣t)
(2)解:①当D在x轴上时,如图2中,

∵QC∥OA,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得t= ![]() .
.
∴t= ![]() s时,点D在x轴上,
s时,点D在x轴上,
②如图,

∵PQ∥AB,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴t= ![]() ,
,
综上所述,当 ![]() <t<
<t< ![]() 时,点D落在△ABO内部(不包括边界)
时,点D落在△ABO内部(不包括边界)
(3)解:如图3中,作QN⊥BC于N,
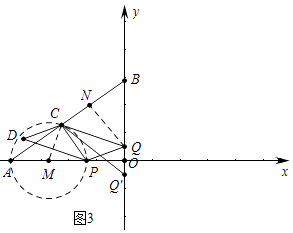
∵Q(0,3﹣2t),Q′(0,2t﹣3),
当QC与⊙M相切时,则QC⊥CM,
∴∠QCM=90°,∴∠QCP+∠PCM=90°,∵∠QCP+∠QCB=90°,
∴∠BCQ=∠PCM=∠CPM,
∵∠CPM+∠PAC=90°,∠OBA+∠OAB=90°,
∴∠APC=∠OBA,∴∠QBC=∠QCB,
∴BQ=CQ,
∵cos∠ABO= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得t= ![]() ,
,
当CQ′是⊙M切线时,同法可得 ![]() =
= ![]() ,
,
解得t= ![]() ,
,
∴t= ![]() s或
s或 ![]() 时,过A,P,C三点的圆与△CQQ′三边中的一条边相切
时,过A,P,C三点的圆与△CQQ′三边中的一条边相切
【解析】(1)利用三角函数sin∠OAB= ![]() =
= ![]() ,cos∠OAB=
,cos∠OAB= ![]() =
= ![]() ,列出关系式即可解决问题.(2)①当D在x轴上时,如图2中,由QC∥OA,得
,列出关系式即可解决问题.(2)①当D在x轴上时,如图2中,由QC∥OA,得 ![]() =
= ![]() ,由此即可解决问题.②当点D在AB上时,如图3中,由PQ∥AB,得
,由此即可解决问题.②当点D在AB上时,如图3中,由PQ∥AB,得 ![]() =
= ![]() ,求出时间t,求出①②两种情形时的△POQ的面积即可解决问题.(3)如图4中,当QC与⊙M相切时,则QC⊥CM,首先证明QB=QC,作QN∠BC于N,根据cos∠ABO=
,求出时间t,求出①②两种情形时的△POQ的面积即可解决问题.(3)如图4中,当QC与⊙M相切时,则QC⊥CM,首先证明QB=QC,作QN∠BC于N,根据cos∠ABO= ![]() =
= ![]() ,列出方程即可解决问题,当CQ′是⊙M切线时,方法类似.
,列出方程即可解决问题,当CQ′是⊙M切线时,方法类似.


科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法: ①2a+b=0;
②当﹣1≤x≤3时,y<0;
③若(x1 , y1)、(x2 , y2)在函数图象上,当x1<x2时,y1<y2
④9a+3b+c=0
其中正确的是( )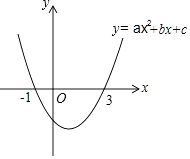
A.①②④
B.①②③
C.①④
D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A是双曲线y= ![]() 在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=
在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y= ![]() (k<0)上运动,则k的值是 .
(k<0)上运动,则k的值是 . 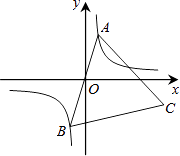
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AC=BC,点D在BC上,作∠ADF=∠B,DF交外角∠ACE的平分线CF于点F.

(1)求证:CF∥AB;
(2)若∠CAD=20°,求∠CFD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
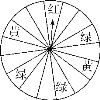
【题目】端午节期间,某商场为了吸引顾客,设立了一个可以自由转动的转盘(转盘被平均分成16份),并规定:顾客每购买100元的商品,就能获得一次转转盘的机会,如果转盘停止后,指针正好对准红色、黄色或绿色区域,顾客就可以分别获得玩具熊、童话书、水彩笔.小明和妈妈购买了125元的商品,请你回答下列问题:
(1)小明获得奖品的概率是多少?
(2)小明获得玩具熊、童话书、水彩笔的概率分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】坐标平面内有4个点A(0,2),B(-2,0),C(1,-1),D(3,1).
(1)建立坐标系,描出这4个点;
(2)顺次连接A,B,C,D,组成四边形ABCD,求四边形ABCD的面积.
(3)线段AB,CD有什么关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平整的地面上,用若干个棱长完全相同的小正方体堆成一个几何体.
(1)请画出这个几何体的三视图.
(2)如果现在你手头还有一些相同的小正方体,要求保持俯视图和左视图不变,最多可以再添加几个小正方体


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径作半圆O交BC于点D,过点D作DE⊥AC,垂足为E. 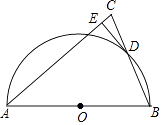
(1)求证:DE是⊙O的切线;
(2)若CE=1,BC=6,求半圆O的半径的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com