
 为了进一步丰富校园文化生活,某校举办了校园文化艺术节.小颖为了了解同学们对这次艺术节的评价,对该校的部分学生进行调查(共有很好、好、一般、不好四种评价),并绘制了如下尚不完整的统计表与扇形统计图.
为了进一步丰富校园文化生活,某校举办了校园文化艺术节.小颖为了了解同学们对这次艺术节的评价,对该校的部分学生进行调查(共有很好、好、一般、不好四种评价),并绘制了如下尚不完整的统计表与扇形统计图.| 评价 | 频数(人) | 频率 |
| 很好 | 20 | |
| 好 | 0.45 | |
| 一般 | ||
| 不好 | 5 |
| 72° |
| 360° |
| 30 |
| 100 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系中,把以格点为顶点的三角形称为格点三角形(每个小方格都是边长为1的正方形),图中△ABC是格点三角形,点A、B、C的坐标分别是(-4,-1)、(-2,-3)、(-1,-2).
如图,在平面直角坐标系中,把以格点为顶点的三角形称为格点三角形(每个小方格都是边长为1的正方形),图中△ABC是格点三角形,点A、B、C的坐标分别是(-4,-1)、(-2,-3)、(-1,-2).查看答案和解析>>
科目:初中数学 来源: 题型:
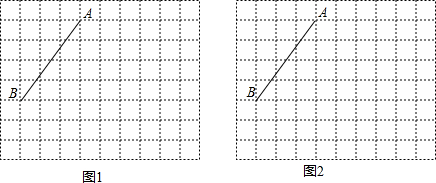
 在三行三列的方格棋盘上沿骰子的某条棱翻动骰子(相对面上分别标有1点和6点,2点和5点,3点和4点).开始时,骰子如图1所示摆放,朝上的点数是2,最后翻动到如图2所示位置.现要求翻动次数最少,则最后骰子朝上的点数为2的概率为
在三行三列的方格棋盘上沿骰子的某条棱翻动骰子(相对面上分别标有1点和6点,2点和5点,3点和4点).开始时,骰子如图1所示摆放,朝上的点数是2,最后翻动到如图2所示位置.现要求翻动次数最少,则最后骰子朝上的点数为2的概率为查看答案和解析>>
科目:初中数学 来源: 题型:
| A、3.286×105 |
| B、3.286×106 |
| C、3.286×107 |
| D、3.286×108 |
查看答案和解析>>
科目:初中数学 来源: 题型:

 |
| GH |
查看答案和解析>>
科目:初中数学 来源: 题型:
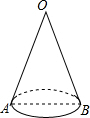 如图是一个圣诞帽,已知开口圆的直径AB长为10cm,母线OA长为20cm.从开口的A点出发,用一根彩带绕侧面一周回到A点,则彩带最短需要( )
如图是一个圣诞帽,已知开口圆的直径AB长为10cm,母线OA长为20cm.从开口的A点出发,用一根彩带绕侧面一周回到A点,则彩带最短需要( )| A、20cm | ||
B、20
| ||
| C、30cm | ||
D、20
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com