
���� ��1������ϴǰ�߲��ϲ�����ũҩ��Ϊ1���ֱ���a�Ĵ���ʽ��ʾ�߲��ϲ�����ũҩ������a��λ����ˮ��ϴһ�Σ���ʾ���߲��ϲ�����ũҩ��ΪM��
��2����a��λ����ˮƽ���ֳ����ݺ���ϴ���Σ���ʾ���߲��ϲ�����ũҩ��N��
��3����������Ƚ�M��N��С���ɵõ������
��� �⣺��1������ϴǰ�߲��ϲ�����ũҩ��Ϊ1���ֱ���a�Ĵ���ʽ��ʾ�߲��ϲ�����ũҩ����
��a��λ����ˮ��ϴһ�Σ��߲��ϲ�����ũҩ��ΪM=$\frac{1}{1+a}$��
�ʴ�Ϊ��$\frac{1}{1+a}$
��2����a��λ����ˮƽ���ֳ����ݺ���ϴ���Σ�
�߲��ϲ�����ũҩ��N=$\frac{1}{1+\frac{a}{2}}$•$\frac{1}{1+\frac{a}{2}}$=$\frac{1}{��1+\frac{a}{2}��^{2}}$��
��3���ߣ�1+a��-��1+$\frac{a}{2}$��2=1+a-1-a-$\frac{{a}^{2}}{4}$=-$\frac{{a}^{2}}{4}$��
��1+a����1+a��2��
��P��Q��
��������ϴ���β�����ũҩ���Ƚ��٣�
���� ���⿼���˷�ʽ�ļӼ������Լ�����Ƚϴ�С����ʾ��M��N�ǽⱾ��Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
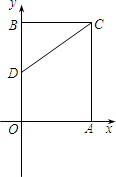 ��ƽ��ֱ������ϵ�У�����OACB�Ķ���O������ԭ�㣬����A��B�ֱ���x��y����������ϣ�OA=3��OB=4��DΪOB���е㣬��EΪ��OA�ϵ�һ�����㣮
��ƽ��ֱ������ϵ�У�����OACB�Ķ���O������ԭ�㣬����A��B�ֱ���x��y����������ϣ�OA=3��OB=4��DΪOB���е㣬��EΪ��OA�ϵ�һ�����㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��������������������ͳ��Ϊ������ | B�� | ����������������0�������� | ||
| C�� | ������3.10��ȷ����ʮ��λ | D�� | -24������-2��ָ����4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
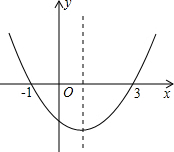 ���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�����н��ۣ���a��0����-$\frac{b}{2a}$=1����b2-4ac��0���ܵ�x��1ʱ��y��x���������С���ݵ�-1��x��3ʱ��y��0��������ȷ���Ǣڢݣ���ֻ����ţ�
���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�����н��ۣ���a��0����-$\frac{b}{2a}$=1����b2-4ac��0���ܵ�x��1ʱ��y��x���������С���ݵ�-1��x��3ʱ��y��0��������ȷ���Ǣڢݣ���ֻ����ţ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ƽ�����ϵĵ㵽�����ߵľ������ | |
| B�� | �߶δ�ֱƽ�����ϵĵ㵽�����߶����˵�ľ������ | |
| C�� | ��ֱ���������У�30������Ե�ֱ�DZߵ���б�ߵ�һ�� | |
| D�� | ƽ���������ڵ����߽��������εĽ�ƽ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x3+x3=2x6 | B�� | x6��x2=x3 | C�� | ��-3x3��2=3x6 | D�� | x3•x2=x5 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com