
分析 首先将原方程变形为:(x+y)2+2y2=81,即可得x+y必须是奇数,然后设x+y=2t+1,可得新方程(2t+1)2+2y2=81,解此方程即可求得答案.
解答 解:x2+2xy+3y2=81,
方程变形得:(x+y)2+2y2=81,
∵81是奇数,2y2是偶数,
∴x+y必须是奇数,
设x+y=2t+1,
则原方程变为:(2t+1)2+2y2=81,
它的整数解为$\left\{\begin{array}{l}{2t+1=±7}\\{y=±4}\end{array}\right.$或$\left\{\begin{array}{l}{2t+1=±3}\\{y=±6}\end{array}\right.$,
则当y=4,2t+1=7时,x=3;
当y=4,2t+1=-7时,x=-11;
当y=-4,2t+1=7时,x=11;
当y=-4,2t+1=-7时,x=-3;
当y=6,2t+1=3时,x=-3;
当y=6,2t+1=-3时,x=-9;
当y=-6,2t+1=3时,x=9;
当y=-6,2t+1=-3时,x=3;
∴方程x2+2xy+3y2=81的整数解(x,y)的组数为8组.
故答案为:8.
点评 此题考查了非一次不定方程的知识.此题难度较大,解题的关键是将原方程变形为:(x+y)2+2y2=81,由x+y必须是奇数,然后设x+y=2t+1,从而得新方程(2t+1)2+2y2=81.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 我们学校教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:30)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )
我们学校教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:30)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )| A. | 7:00 | B. | 7:07 | C. | 7:10 | D. | 7:15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
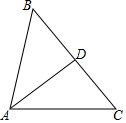 如图,在下列条件中,不能证明△ABD≌△ACD的是( )
如图,在下列条件中,不能证明△ABD≌△ACD的是( )| A. | BD=DC,AB=AC | B. | ∠ADB=∠ADC,BD=DC | C. | ∠B=∠C,∠BAD=∠CAD | D. | ∠B=∠C,BD=DC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +5 | -2 | -4 | +13 | -10 | +16 | -9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com