
【题目】已知一抛物线与x轴的交点是A(﹣2,0)、B(1,0),与y轴的交点是C,且经过点D(2,8).
(1)求该抛物线的解析式;
(2)作出该抛物线的简图(自建坐标系);
(3)在抛物线对称轴上求一点E,使EC+EB最小.
【答案】(1)y=2x2+2x﹣4;(2)抛物线图象如图所示见解析;(3)E(![]() ,﹣3).
,﹣3).
【解析】
(1)设函数的表达式为:y=a(x+2)(x﹣1),将点D的坐标代入上式,即可求解;
(2)根据函数表达式描点、画图即可;
(3)点A是点B关于函数对称轴的对称点,连接AC交函数对称轴于点E,点E为所求点,求出直线AC的解析式,即可得到点E坐标.
(1)设函数的表达式为:y=a(x+2)(x﹣1),
将点D的坐标代入上式得:8=a(2+2)(2﹣1),
解得:a=2,
故抛物线的表达式为:y=2(x+2)(x﹣1)=2x2+2x﹣4;
(2)抛物线图象如下图:

(3)由题意可得:抛物线对称轴为:![]() ,C(0,-4),
,C(0,-4),
点A是点B关于函数对称轴的对称点,连接AC交函数对称轴于点E,点E为所求点,
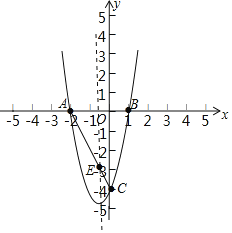
设直线AC的解析式为:y=kx+b,
将点A、C的坐标代入得:![]() ,解得:
,解得:![]() ,
,
故直线AC的表达式为:y=﹣2x﹣4,
当x=﹣![]() 时,y=﹣3,则点E(﹣
时,y=﹣3,则点E(﹣![]() ,﹣3).
,﹣3).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
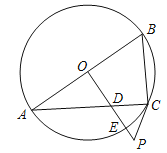
【题目】如图,已知AB是⊙O的直径,过O点作OP⊥AB,交弦AC于点D,交⊙O于点E,且使∠PCA=∠ABC.
(1)求证:PC是⊙O的切线;
(2)若∠P=60°,PC=2,求PE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某种新商品每件进价是![]() ,在试销期间发现,当每件商品售价为
,在试销期间发现,当每件商品售价为![]() 元时,每天可销售
元时,每天可销售![]() 件,当每件商品售价高于
件,当每件商品售价高于![]() 元时,每涨价
元时,每涨价![]() 元,日销售量就减少
元,日销售量就减少![]() 件.据此规律,请回答:
件.据此规律,请回答:
(1)当每件商品售价定为![]() 元时,每天可销售多少件商品,商场获得的日盈利是多少?
元时,每天可销售多少件商品,商场获得的日盈利是多少?
(2)在上述条件不变,商品销售正常的情况下,每件商品的销售价定为多少元时,商场日盈利可达到![]() 元?(提示:盈利
元?(提示:盈利![]() 售价
售价![]() 进价)
进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小琴的父母承包了一块荒山地种植一批梨树,今年收获一批金溪密梨,小琴的父母打算以m元/斤的零售价销售5000斤密梨;剩余的5000(m+1)斤密犁以比零售价低1元的批发价批给外地客商,预计总共可赚得55 000元的毛利润.

(1)求小琴的父母今年共收获金溪密梨多少斤?
(2)若零售金溪密梨平均每天可售出200斤,每斤盈利2元.为了加快销售和获得较好的售价,采取了降价措施,发现销售单价每降低0.1元,平均每天可多售出40斤,应降价多少元?每天销售利润为600元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(﹣2,﹣4),O(0,0),B(2,0)三点.
(1)求抛物线y=ax2+bx+c的解析式;
(2)若点M是该抛物线对称轴上的一点,求AM+OM的最小值.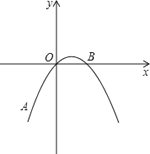
查看答案和解析>>
科目:初中数学 来源: 题型:
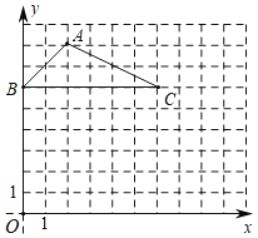
【题目】如图,在平面直角坐标系中,△ABC的顶点都在小方格的格点上.
(1)点A的坐标是 ;点C的坐标是 ;
(2)以原点O为位似中心,将△ABC缩小,使变换后得到的△A1B1C1与△ABC对应边的比为1:2,请在网格中画出△A1B1C1;
(3)△A1B1C1的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高学生的阅读兴趣,某学校建立了共享书架,并购买了一批书籍.其中购买![]() 种图书花费了3000元,购买
种图书花费了3000元,购买![]() 种图书花费了1600元,A种图书的单价是
种图书花费了1600元,A种图书的单价是![]() 种图书的1.5倍,购买
种图书的1.5倍,购买![]() 种图书的数量比
种图书的数量比![]() 种图书多20本.
种图书多20本.
(1)求![]() 和
和![]() 两种图书的单价;
两种图书的单价;
(2)书店在“世界读书日”进行打折促销活动,所有图书都按8折销售学校当天购买了![]() 种图书20本和
种图书20本和![]() 种图书25本,共花费多少元?
种图书25本,共花费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-6x+8.求:
(1)抛物线与x轴和y轴相交的交点坐标;
(2)抛物线的顶点坐标;
(3)画出此抛物线图象,利用图象回答下列问题:
①方程x2-6x+8=0的解是什么?
②x取什么值时,函数值大于0?
③x取什么值时,函数值小于0?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com