
����Ŀ���̳�ij������Ʒÿ��������![]() ���������ڼ䷢�֣���ÿ����Ʒ�ۼ�Ϊ
���������ڼ䷢�֣���ÿ����Ʒ�ۼ�Ϊ![]() Ԫʱ��ÿ�������
Ԫʱ��ÿ�������![]() ������ÿ����Ʒ�ۼ۸���
������ÿ����Ʒ�ۼ۸���![]() Ԫʱ��ÿ�Ǽ�
Ԫʱ��ÿ�Ǽ�![]() Ԫ�����������ͼ���
Ԫ�����������ͼ���![]() ��.�ݴ˹��ɣ���ش�
��.�ݴ˹��ɣ���ش�
��1����ÿ����Ʒ�ۼ۶�Ϊ![]() Ԫʱ��ÿ������۶��ټ���Ʒ���̳���õ���ӯ���Ƕ��٣�
Ԫʱ��ÿ������۶��ټ���Ʒ���̳���õ���ӯ���Ƕ��٣�
��2���������������䣬��Ʒ��������������£�ÿ����Ʒ�����ۼ۶�Ϊ����Ԫʱ���̳���ӯ���ɴﵽ![]() Ԫ������ʾ��ӯ��
Ԫ������ʾ��ӯ��![]() �ۼ�
�ۼ�![]() ���ۣ�
���ۣ�
���𰸡���1��ÿ�������![]() ����Ʒ���̳���õ���ӯ����
����Ʒ���̳���õ���ӯ����![]() Ԫ����2��ÿ����Ʒ�ۼ�Ϊ
Ԫ����2��ÿ����Ʒ�ۼ�Ϊ![]() Ԫʱ���̳���ӯ���ﵽ
Ԫʱ���̳���ӯ���ﵽ![]() Ԫ.
Ԫ.
��������
��1���������ÿ���������Ʒ������Ȼ��������ӯ����
��2�����̳���ӯ���ﵽ1600Ԫʱ��ÿ����Ʒ�ۼ�ΪxԪ������ÿ����Ʒ��ӯ�������۵ļ���=�̳�����ӯ�����з�����⼴�ɣ�
�⣺��1����ÿ����Ʒ�ۼ�Ϊ![]() Ԫʱ����ÿ����Ʒ�ۼ�
Ԫʱ����ÿ����Ʒ�ۼ�![]() Ԫ�߳�
Ԫ�߳�![]() Ԫ��
Ԫ��
��![]() ��Ԫ����
��Ԫ����
��ÿ���������Ʒ![]() ������
������![]() ��������
��������
�̳��ɻ���ӯ��Ϊ![]() ��Ԫ����
��Ԫ����
��ÿ�������![]() ����Ʒ���̳���õ���ӯ����
����Ʒ���̳���õ���ӯ����![]() Ԫ
Ԫ
��2�����̳���ӯ���ﵽ![]() Ԫʱ��ÿ����Ʒ�ۼ�Ϊ
Ԫʱ��ÿ����Ʒ�ۼ�Ϊ![]() Ԫ��
Ԫ��
��ÿ����Ʒ��![]() Ԫ�߳�
Ԫ�߳�![]() Ԫ��ÿ����ӯ��
Ԫ��ÿ����ӯ��![]() Ԫ
Ԫ
ÿ��������ƷΪ![]() ������
������
������÷���![]()
��������![]() ����
����![]()
���![]()
��ÿ����Ʒ�ۼ�Ϊ![]() Ԫʱ���̳���ӯ���ﵽ
Ԫʱ���̳���ӯ���ﵽ![]() Ԫ.
Ԫ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ����ﴫͳ�Ļ�����������У����У�ѧУ�ƻ���չ��������A����ѧ�ж�������B���ݽ�������C���α��硱����D���鷨����Ҫ��ÿλͬѧ������ֻ�ܲμ�����һ����ѧУΪ���˽�ѧ������Ը����������˲���ѧ�������ͳ�����£�
��1����ͼ��ϣ���μӻCռ20%��ϣ���μӻBռ15%�������������Ϊ �ˣ�����ͳ��ͼ�У�ϣ���μӻD��ռԲ�Ľ�Ϊ �ȣ�����������Ϣ��ȫ����ͳ��ͼ��
��2��ѧУ����800��ѧ���������ͼ����Ϣ������ȫУѧ��ϣ���μӻA�ж����ˣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ1��һ������վ��ڵ�˫��բ������ͼ2������˫��չ��ʱ��˫����Ե�Ķ˵�A��B֮��ľ���Ϊ10cm��˫���ı�ԵAC��BD��54cm������բ��������нǡ�PCA����BDQ��30�㣮��˫������ʱ������ͨ��բ���������������Ϊ(����)

A. (54![]() +10) cm B. (54
+10) cm B. (54![]() +10) cm C. 64 cm D. 54cm
+10) cm C. 64 cm D. 54cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������![]() �ĶԳ���Ϊֱ��
�ĶԳ���Ϊֱ��![]() ������������
������������![]() �ύ��
�ύ��![]() ��
��![]() ���㣬��
���㣬��![]() �ύ��
�ύ��![]() �㣬����
�㣬����![]() ��
��![]() .
.

��1����ֱ��![]() ����
����![]() ��
��![]() ���㣬��ֱ��
���㣬��ֱ��![]() �������ߵĽ���ʽ��
�������ߵĽ���ʽ��
��2���������ߵĶԳ���![]() ����һ��
����һ��![]() ��ʹ��
��ʹ��![]() ����
����![]() �ľ����뵽��
�ľ����뵽��![]() �ľ���֮����С�������
�ľ���֮����С�������![]() �����ꣻ
�����ꣻ
��3�����![]() Ϊ�����ߵĶԳ���
Ϊ�����ߵĶԳ���![]() �ϵ�һ�����㣬��ʹ
�ϵ�һ�����㣬��ʹ![]() Ϊֱ�������εĵ�
Ϊֱ�������εĵ�![]() ������.
������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��װ������ijƷ�Ƶ�T�����ɱ���ÿ��10Ԫ�������г����飬�Ե���13Ԫ������������������Ը�⾭��5000�������ұ�ʾÿ����0.1Ԫ��Ը��ྭ��500������װ�������������ڲ�����11.4Ԫ��ǰ���£����������½�0.1xԪ.
��1����������y��x�Ĺ�ϵ�������x��ȡֵ��Χ��
��2���������������أ����ʳ������������Ƕ���ʱ��������W��������������Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
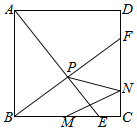
����Ŀ����ͼ��������ABCD�ı߳�Ϊ2����E����F�ֱ��DZ�BC����CD�ϵĶ��㣬��BE��CF��AE��BF�ཻ�ڵ�P������MΪ��BC���е㣬��NΪ��CD������һ�㣬��MN+PN����Сֵ����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
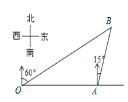
����Ŀ����ͼ���ۿ�A�ڹ۲�վO����������OA=6��ij���Ӹۿ�A�������ر�ƫ��15��������һ�ξ����B������ʱ�ӹ۲�վO����øô�λ�ڱ�ƫ��60���ķ�����ô����еľ���(��AB�ij�)Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABCD������B��һ��ֱ��1��������ABCD�ĶԽ���AC����ֱ���ཻ�ڵ�G������C��A�ֱ���ֱ��1�Ĵ��߶�CE��AF�ڵ�E��F���Խ���AC��BD�ཻ�ڵ�O������OE��OF��
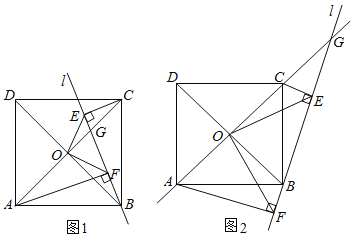
��1����ͼ1���²�OE��OF��������������ϵ��λ�ù�ϵ����˵�����ɣ�
��2���������α߳�Ϊ10��
����ֱ��1����ͼ1��λ�ã���![]() ʱ����EG�ij���
ʱ����EG�ij���
����ֱ��1����ͼ2��λ�ã���![]() ʱ����ֱ��д��EG�ij���
ʱ����ֱ��д��EG�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����У��ȫ��Խ��Խ�ܵ����ǵĹ�ע������ij��ѧ�Բ���ѧ����У��ȫ֪ʶ���˽�̶ȣ����������������ķ�ʽ���������ռ�������Ϣ����ͳ�ƣ����������������в�������ͳ��ͼ������ͼ����Ϣ�ش��������⣺
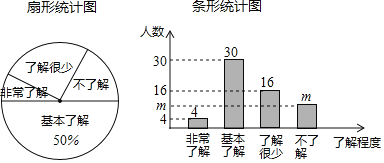
��1�������ʾ������ѧ������______�ˣ�����ͳ��ͼ��m��ֵΪ______��
��2������ͳ��ͼ�����˽��������������Ӧ���ε�Բ�ĽǵĶ���Ϊ______��
��3��������ѧ����ѧ��1800�ˣ��������������������Թ��Ƴ���ѧУѧ���ж�У��ȫ֪ʶ�ﵽ���dz��˽������������˽����̶ȵ�������Ϊ______�ˣ�
��4�����Ӷ�У��ȫ֪ʶ�ﵽ���dz��˽����̶ȵ�2��������2��Ů���������ȡ2�˲μ�У��ȫ֪ʶ�����������б�����״ͼ�ķ�������ǡ�ó鵽1��������1��Ů���ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com