
【题目】“校园安全”越来越受到人们的关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.根据图中信息回答下列问题:
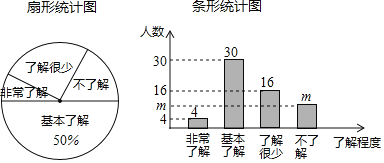
(1)接受问卷调查的学生共有______人,条形统计图中m的值为______;
(2)扇形统计图中“了解很少”部分所对应扇形的圆心角的度数为______;
(3)若该中学共有学生1800人,根据上述调查结果,可以估计出该学校学生中对校园安全知识达到“非常了解”和“基本了解”程度的总人数为______人;
(4)若从对校园安全知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加校园安全知识竞赛,请用列表或画树状图的方法,求恰好抽到1名男生和1名女生的概率.
【答案】(1)60,10;(2)96°;(3)1020;(4)![]()
【解析】
(1)根据基本了解的人数以及所占的百分比可求得接受调查问卷的人数,进行求得不了解的人数,即可求得m的值;
(2)用360度乘以“了解很少”的比例即可得;
(3)用“非常了解”和“基本了解”的人数和除以接受问卷的人数,再乘以1800即可求得答案;
(4)画树状图表示出所有可能的情况数,再找出符合条件的情况数,利用概率公式进行求解即可.
(1)接受问卷调查的学生共有![]() (人),
(人),![]() ,
,
故答案为:60,10;
(2)扇形统计图中“了解很少”部分所对应扇形的圆心角的度数![]() ,
,
故答案为:96°;
(3)该学校学生中对校园安全知识达到“非常了解”和“基本了解”程度的总人数为:![]() (人),
(人),
故答案为:1020;
(4)由题意列树状图:

由树状图可知,所有等可能的结果有12种,恰好抽到1名男生和1名女生的结果有8种,
∴恰好抽到1名男生和1名女生的概率为![]() .
.


科目:初中数学 来源: 题型:
【题目】商场某种新商品每件进价是![]() ,在试销期间发现,当每件商品售价为
,在试销期间发现,当每件商品售价为![]() 元时,每天可销售
元时,每天可销售![]() 件,当每件商品售价高于
件,当每件商品售价高于![]() 元时,每涨价
元时,每涨价![]() 元,日销售量就减少
元,日销售量就减少![]() 件.据此规律,请回答:
件.据此规律,请回答:
(1)当每件商品售价定为![]() 元时,每天可销售多少件商品,商场获得的日盈利是多少?
元时,每天可销售多少件商品,商场获得的日盈利是多少?
(2)在上述条件不变,商品销售正常的情况下,每件商品的销售价定为多少元时,商场日盈利可达到![]() 元?(提示:盈利
元?(提示:盈利![]() 售价
售价![]() 进价)
进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知顶点为D的抛物线![]() 与x轴交于A(-1,0),C(3,0)两点,与y轴交于B点.
与x轴交于A(-1,0),C(3,0)两点,与y轴交于B点.
(1)求该抛物线的解析式及点D坐标;
(2)若点Q是该抛物线的对称轴上的一个动点,当AQ+QB最小时,直接写出直线AQ的函数解析式;
(3)若点P为抛物上的一个动点,且点P在x轴上方,过P作PK垂直x轴于点K,是否存在点P使得A,K,P三点形成的三角形与△DBC相似?如存在,求出点P的坐标,如不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
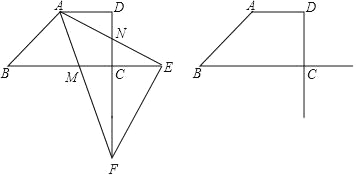
【题目】如图,梯形ABCD中,AD∥BC,DC⊥BC,且∠B=45°,AD=DC=1,点M为边BC上一动点,联结AM并延长交射线DC于点F,作∠FAE=45°交射线BC于点E、交边DCN于点N,联结EF.
(1)当CM:CB=1:4时,求CF的长.
(2)设CM=x,CE=y,求y关于x的函数关系式,并写出定义域.
(3)当△ABM∽△EFN时,求CM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与函数y=![]() (x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=
(x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=![]() OC,且△ACD的面积是6,连接BC.
OC,且△ACD的面积是6,连接BC.
(1)求m,k,n的值;
(2)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).

请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数;
(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个.用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
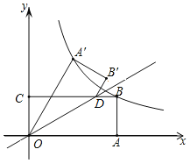
【题目】如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应).若AB=1,反比例函数y=![]() (k≠0)的图象恰好经过点A′,B,则k的值为______.
(k≠0)的图象恰好经过点A′,B,则k的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
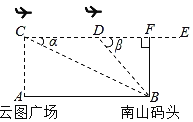
【题目】兴隆湖是成都天府新区著名的生态绿地工程.在一次户外综合实践活动中,小明同学所在的兴趣小组用无人机航拍测量云图广场A与南山码头B的直线距离.由于无人机控制距离有限,为了安全,不能直接测量,他们采用如下方法:如图,小明在云图广场A的正上方点C处测得南山码头B的俯角α=17.09°;接着无人机往南山码头B方向水平飞行0.9千米到达点D处,测得此时南山码头B的俯角β=45°.已知AC⊥AB,CD∥AB,请根据测量数据计算A,B两地的距离.(结果精确到0.1km,参考数据:sinα≈0.29,tanα≈0.31,sinβ≈0.71)
查看答案和解析>>
科目:初中数学 来源: 题型:
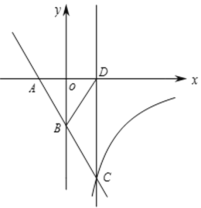
【题目】已知直线:y1=![]() 与x轴、y轴相交于A、B两点,与双曲线
与x轴、y轴相交于A、B两点,与双曲线![]() (k<0,x>0)相交于第四象限的点C,过点C作直线l⊥x轴,垂足为D,若△ABD的面积为
(k<0,x>0)相交于第四象限的点C,过点C作直线l⊥x轴,垂足为D,若△ABD的面积为![]() ,且B是AC的中点.
,且B是AC的中点.
(1)求k的值;
(2)直接写出![]() 的解集;
的解集;
(3)若P为直线l的一动点,点P的纵坐标为m,∠APB≥30°,求m的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com