
【题目】如图,在![]() 中,已知
中,已知![]() ,
,![]() ,且
,且![]() ,将
,将![]() 与
与![]() 重合在一起,若
重合在一起,若![]() 位置保持不动,滑动
位置保持不动,滑动![]() ,且使点
,且使点![]() 在边
在边![]() 上沿
上沿![]() 到
到![]() 的方向运动,
的方向运动,![]() 始终经过点
始终经过点![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
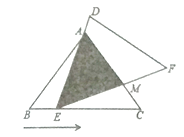
(1)若![]() ,求
,求![]() 的长;
的长;
(2)探究:当![]() 离开
离开![]() 后,
后,![]() 在其它运动过程中,重叠部分(即
在其它运动过程中,重叠部分(即![]() )能否构成等腰三角形?若能,求出
)能否构成等腰三角形?若能,求出![]() 的长;若不能,请说明理由.
的长;若不能,请说明理由.
科目:初中数学 来源: 题型:
【题目】城市中“打车难”一直是人们关注的一个社会热点问题.近几年来,“互联网+”战略与传统出租车行业深度融合,“优步”、“滴滴出行”等打车软件就是其中典型的应用,名为“数据包络分析”(简称DEA)的一种效率评价方法,可以很好地优化出租车资源配置,为了解出租车资源的“供需匹配”,北京、上海等城市对每天24个时段的DEA值进行调查,调查发现,DEA值越大,说明匹配度越好.在某一段时间内,北京的DEA值y与时刻t的关系近似满足函数关系![]() (a,b,c是常数,且
(a,b,c是常数,且![]() ≠0),如图记录了3个时刻的数据,根据函数模型和所给数据,当“供需匹配”程度最好时,最接近的时刻t是( )
≠0),如图记录了3个时刻的数据,根据函数模型和所给数据,当“供需匹配”程度最好时,最接近的时刻t是( )

A. 4.8 B. 5 C. 5.2 D. 5.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)某学校“智慧方园”数学社团遇到这样一个题目:
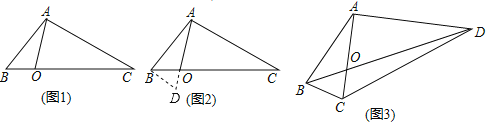
如图1,在△ABC中,点O在线段BC上,∠BAO=30°,∠OAC=75°,AO=![]() ,BO:CO=1:3,求AB的长.
,BO:CO=1:3,求AB的长.
经过社团成员讨论发现,过点B作BD∥AC,交AO的延长线于点D,通过构造△ABD就可以解决问题(如图2).
请回答:∠ADB= °,AB= .
(2)请参考以上解决思路,解决问题:
如图3,在四边形ABCD中,对角线AC与BD相交于点O,AC⊥AD,AO=![]() ,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长.
,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(-3,-3),B(-1,-3)C(-1, 0).

(1)画出△ABC
(2)画出△ABC关于x轴对称的![]() ,并写出点
,并写出点![]() 的坐标:
的坐标:
(3)以点O为位似中心,在第一象限内把△ABC放大到原来的两倍后得到![]() ,写出点
,写出点![]() 的坐标:
的坐标:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“泥兴陶,,是钦州的一张文化名片。钦州市某妮兴陶公司以每只60元的价格销售一种成本价为40元的文化纪念杯,每星期可售出100只。后来经过市场调查发现,每只杯子的售价每降低1元,则平均何星期可多买出10只。若该公司销售这种文化纪念杯要想平均每星期获利2240元,请回答:
(1)每只杯应降价多少元?
(2)在平均每星期获利不变的情况下,为尽可能让利于顾客,赢得市场,该公司应该按原售价的几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
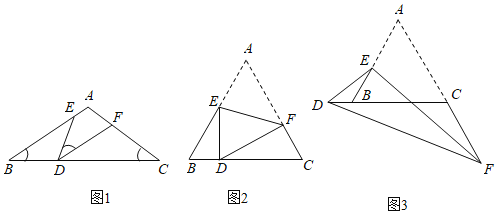
【题目】(1)模型探究:如图1,D、E、F分别为△ABC三边BC、AB、AC上的点,且∠B=∠C=∠EDF=a.△BDE与△CFD相似吗?请说明理由;
(2)模型应用:△ABC为等边三角形,其边长为8,E为AB边上一点,F为射线AC上一点,将△AEF沿EF翻折,使A点落在射线CB上的点D处,且BD=2.
①如图2,当点D在线段BC上时,求![]() 的值;
的值;
②如图3,当点D落在线段CB的延长线上时,求△BDE与△CFD的周长之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象过点
的图象过点![]() 、顶点
、顶点![]() 的横坐标为.
的横坐标为.
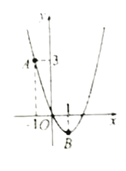
(1)求这个二次函数的解析式;
(2)点![]() 在该一次函数的图象上,点
在该一次函数的图象上,点![]() 在
在![]() 轴上,若以
轴上,若以![]() 为顶点的四边形是平行四边形,求点
为顶点的四边形是平行四边形,求点![]() 的坐标。
的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com