
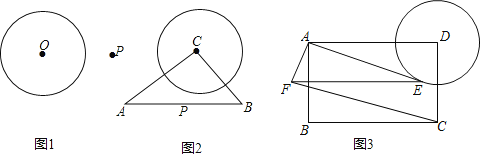
【题目】(1)如图1,A是⊙O上一动点,P是⊙O外一点,在图中作出PA最小时的点A.
(2)如图2,Rt△ABC中,∠C=90°,AC=8,BC=6,以点C为圆心的⊙C的半径是3.6,Q是⊙C上一动点,在线段AB上确定点P的位置,使PQ的长最小,并求出其最小值.
(3)如图3,矩形ABCD中,AB=6,BC=9,以D为圆心,3为半径作⊙D,E为⊙D上一动点,连接AE,以AE为直角边作Rt△AEF,∠EAF=90°,tan∠AEF=![]() ,试探究四边形ADCF的面积是否有最大或最小值,如果有,请求出最大或最小值,否则,请说明理由.
,试探究四边形ADCF的面积是否有最大或最小值,如果有,请求出最大或最小值,否则,请说明理由.
【答案】(1)作图见解析;(2)PQ长最短是1.2;(3)四边形ADCF面积最大值是![]() ,最小值是
,最小值是![]() .
.
【解析】
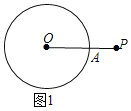
(1)连接线段OP交⊙C于A,点A即为所求;
(2)过C作CP⊥AB于Q,P,交⊙C于Q,这时PQ最短,根据勾股定理以及三角形的面积公式即可求出其最小值;
(3)△ACF的面积有最大和最小值,取AB的中点G,连接FG,DE,证明△FAG~△EAD,进而证明点F在以G为圆心1为半径的圆上运动,过G作GH⊥AC于H,交⊙G于F1,GH反向延长线交⊙G于F2,①当F在F1时,△ACF面积最小,分别求出△ACD的面积和△ACF的面积的最小值即可得出四边形ADCF的面积的最小值;②当F在F2时,四边形ADCF的面积有最大值,在⊙G上任取异于点F2的点P,作PM⊥AC于M,作GN⊥PM于N,利用矩形的判定与性质以及三角形的面积公式即可得出得出四边形ADCF的面积的最大值.
解:(1)连接线段OP交⊙C于A,点A即为所求,如图1所示;
(2)过C作CP⊥AB于Q,P,交⊙C于Q,这时PQ最短.
理由:分别在线段AB,⊙C上任取点P',点Q',连接P',Q',CQ',如图2,
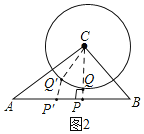
由于CP⊥AB,根据垂线段最短,CP≤CQ'+P'Q',
∴CO+PQ≤CQ'+P'Q',
又∵CQ=CQ',
∴PQ<P'Q',即PQ最短.
在Rt△ABC中![]() ,
,![]() ,
,
∴![]() ,
,
∴PQ=CP﹣CQ=6.8﹣3.6=1.2,
∴![]() .
.
当P在点B左侧3.6米处时,PQ长最短是1.2.
(3)△ACF的面积有最大和最小值.
如图3,取AB的中点G,连接FG,DE.
∵∠EAF=90°,![]() ,
,
∴![]()
∵AB=6,AG=GB,
∴AC=GB=3,
又∵AD=9,
∴![]() ,
,
∴![]()
∵∠BAD=∠B=∠EAF=90°,
∴∠FAG=∠EAD,
∴△FAG~△EAD,
∴![]() ,
,
∵DE=3,
∴FG=1,
∴点F在以G为圆心1为半径的圆上运动,
连接AC,则△ACD的面积=![]() ,
,
过G作GH⊥AC于H,交⊙G于F1,GH反向延长线交⊙G于F2,
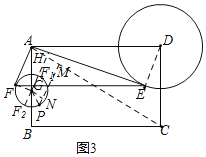
①当F在F1时,△ACF面积最小.理由:由(2)知,当F在F1时,F1H最短,这时△ACF的边AC上的高最小,所以△ACF面积有最小值,
在Rt△ABC中,![]()
∴![]() ,
,
在Rt△ACH中,![]() ,
,
∴![]() ,
,
∴△ACF面积有最小值是:![]() ;
;
∴四边形ADCF面积最小值是:![]() ;
;
②当F在F2时,F2H最大理由:在⊙G上任取异于点F2的点P,作PM⊥AC于M,作GN⊥PM于N,连接PG,则四边形GHMN是矩形,
∴GH=MN,
在Rt△GNP中,∠NGF2=90°,
∴PG>PN,
又∵F2G=PG,
∴F2G+GH>PN+MN,即F2H>PM,
∴F2H是△ACF的边AC上的最大高,
∴面积有最大值,
∵![]() ,
,
∴△ACF面积有最大值是![]() ;
;
∴四边形ADCF面积最大值是![]() ;
;
综上所述,四边形ADCF面积最大值是![]() ,最小值是
,最小值是![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
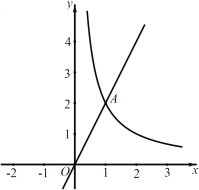
【题目】如图,直线![]() 与函数
与函数![]()
![]() 的图象交于点
的图象交于点![]() .
.
(1)求![]() 的值;
的值;
(2)过点![]() 作
作![]() 轴的平行线
轴的平行线![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,与函数
,与函数![]()
![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
①若点![]() 是线段
是线段![]() 的中点时,则点
的中点时,则点![]() 的坐标是______,
的坐标是______,![]() 的值是______;(直接写答案)
的值是______;(直接写答案)
②当![]() 时,直接写出
时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
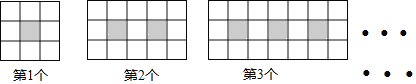
【题目】如图,每个图案均由边长相等的黑、白两色正方形按规律拼接而成,照此规律,第n个图案中白色正方形比黑色正方形多________个.(用含n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
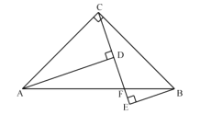
【题目】已知:在![]() 中,
中,![]() ,
,![]() ,过点
,过点![]() 、
、![]() 向过点
向过点![]() 的直线作垂线,垂足分别为
的直线作垂线,垂足分别为![]() 、
、![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
(1)如图,求证:![]() ;
;
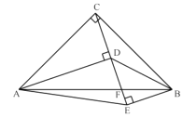
(2)如图,连接![]() 、
、![]() ,若
,若![]() ,在不添加任何辅助线的情况下,请直接写出四个角,使写出的每一个角的正切值都等于
,在不添加任何辅助线的情况下,请直接写出四个角,使写出的每一个角的正切值都等于![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
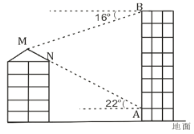
【题目】如图,小明在商城二楼地板![]() 处发现对五层居民楼顶防雨棚一侧斜面
处发现对五层居民楼顶防雨棚一侧斜面![]() 与点
与点![]() 在一条直线上,此时测得
在一条直线上,此时测得![]() ,
,![]() 仰角是
仰角是![]() ,上到九楼在地板边沿
,上到九楼在地板边沿![]() 点测得居民楼顶斜面顶端
点测得居民楼顶斜面顶端![]() 点俯角是
点俯角是![]() ,已知商城每层楼高
,已知商城每层楼高![]() 米,居民楼每层楼高
米,居民楼每层楼高![]() 米,试计算居民楼顶防雨棚一侧斜面
米,试计算居民楼顶防雨棚一侧斜面![]() 的长度.(结果保留精确到
的长度.(结果保留精确到![]() 米)(参考数据:
米)(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
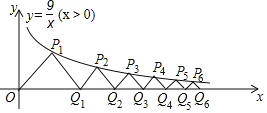
【题目】如图,在平面直角坐标系xOy中,点P1(x1,y1)、P2(x2,y2)、P3(x3,y3),……,Pn(xn,yn)均在反比例函数y=![]() (x>0)的图象上,点Q1、Q2、Q3、……、Qn均在x轴的正半轴上,且△OP1Q1、△Q1P2Q2、△Q2P3Q3、…、△Qn﹣1PnQn均为等腰直角三角形,OQ1、Q1Q2、Q2Q3、……、Qn﹣1Qn分别为以上等腰直角三角形的底边,则y1+y2+y3+…+y2019的值等于_____.
(x>0)的图象上,点Q1、Q2、Q3、……、Qn均在x轴的正半轴上,且△OP1Q1、△Q1P2Q2、△Q2P3Q3、…、△Qn﹣1PnQn均为等腰直角三角形,OQ1、Q1Q2、Q2Q3、……、Qn﹣1Qn分别为以上等腰直角三角形的底边,则y1+y2+y3+…+y2019的值等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国古代有若辉煌的数学成就,《周髀算经》,《九章算术》,《海岛算经》(分别用字母A、B、C依次表示这三部专著)等是我国古代数学的重要文献.将A、B、C这三个字母分别写在3张完全相同的不透明卡片的正面上,把这3张卡片背面朝上洗均后放在桌面上小明先从中随机抽取张卡片,记录下卡片上的字母,放回后洗均,再由小强从中随机抽取张卡片,请用列表法或画树状图法,求小明和小强抽到的卡片上的字母相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点B的坐标为(3,0),将直线
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点B的坐标为(3,0),将直线![]() 沿y轴向上平移3个单位长度后恰好经过B、C两点.
沿y轴向上平移3个单位长度后恰好经过B、C两点.
(1)求直线BC及抛物线的解析式;
(2)设抛物线的顶点为D,点P在抛物线的对称轴上,且![]() ,求点P的坐标;
,求点P的坐标;
(3)连结CD,求∠OCA与∠OCD两角和的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com