
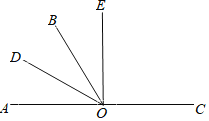
【题目】如图,O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内,且∠DOE=60°,∠BOE=![]() ∠EOC,则下列四个结论正确的个数有( )
∠EOC,则下列四个结论正确的个数有( )
①∠BOD=30°;②射线OE平分∠AOC;③图中与∠BOE互余的角有2个;④图中互补的角有6对.
A.1个B.2个C.3个D.4个
【答案】D
【解析】
根据题意首先计算出∠AOD的度数,再计算出∠AOE、∠EOC、∠BOE、∠BOD的度数,然后再分析即可.
解:由题意设∠BOE=x,∠EOC=3x,
∵∠DOE=60°,OD平分∠AOB,
∴∠AOD=∠BOD =60°-x,
根据题意得:2(60°-x)+4x=180°,解得x=30°,
∴∠EOC=∠AOE=90°,∠BOE=30°,
∴∠BOD=∠AOD=30°,故①正确;
∵∠BOD=∠AOD=30°,
∴射线OE平分∠AOC,故②正确;
∵∠BOE=30°,∠AOB=60°,∠DOE=60°,
∴∠AOB+∠BOE=90°,∠BOE+∠DOE=90°,
∴图中与∠BOE互余的角有2个,故③正确;
∵∠AOE=∠EOC=90°,
∴∠AOE+∠EOC=180°,
∵∠EOC=90°,∠DOB=30°,∠BOE=30°,∠AOD=30°,
∴∠COD+∠AOD=180°,∠COD+∠BOD=180°,∠COD+∠BOE=180°,∠COB+∠AOB=180°,∠COB+∠DOE=180°,
∴图中互补的角有6对,故④正确,
正确的有4个,
故选:D.


 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案科目:初中数学 来源: 题型:
【题目】先化简再求值:
(1)[(xy+2)(xy﹣2)﹣2x2y2+4]÷(xy),其中x=10,y=![]()
(2)(x+2y)2﹣(x+y)(3x﹣y)﹣5y2,其中x=﹣2,y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对某一个函数给出如下定义:若存在实数![]() ,对于函数图象上横坐标之差为1的任意两点
,对于函数图象上横坐标之差为1的任意两点![]() ,
,![]() ,
,![]() 都成立,则称这个函数是限减函数,在所有满足条件的
都成立,则称这个函数是限减函数,在所有满足条件的![]() 中,其最大值称为这个函数的限减系数.例如,函数
中,其最大值称为这个函数的限减系数.例如,函数![]() ,当
,当![]() 取值
取值![]() 和
和![]() 时,函数值分别为
时,函数值分别为![]() ,
,![]() ,故
,故![]() ,因此函数
,因此函数![]() 是限减函数,它的限减系数为
是限减函数,它的限减系数为![]() .
.
(1)写出函数![]() 的限减系数;
的限减系数;
(2)![]() ,已知
,已知![]() (
(![]() )是限减函数,且限减系数
)是限减函数,且限减系数![]() ,求
,求![]() 的取值范围.
的取值范围.
(3)已知函数![]() 的图象上一点
的图象上一点![]() ,过点
,过点![]() 作直线
作直线![]() 垂直于
垂直于![]() 轴,将函数
轴,将函数![]() 的图象在点
的图象在点![]() 右侧的部分关于直线
右侧的部分关于直线![]() 翻折,其余部分保持不变,得到一个新函数的图象,如果这个新函数是限减函数,且限减系数
翻折,其余部分保持不变,得到一个新函数的图象,如果这个新函数是限减函数,且限减系数![]() ,直接写出
,直接写出![]() 点横坐标
点横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自相车厂一周计划生产1400自行车,平均每天生产200量,由于各种原因实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产为正,减产为负);
![]()
(1)根据记录可知前三天共生产 辆;
(2)产量最多的一天比产量最少的一天多生产 辆;
(3)该厂实行计件工资制,每辆车60元,超额完成任务每辆奖15元,少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
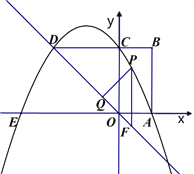
【题目】如图,在矩形OABC中,点A,点C分别在x轴和y轴上,点B(1,2).抛物线y=ax2+bx+c经过点A、C,交BC延长线于D,与x轴另一个交点为E,且AE=4.
(1)求抛物线的表达式;
(2)点P是直线OD上方抛物线上的一个动点,PF∥y轴,PQ⊥OD,垂足为Q.
①猜想:PQ与FQ的数量关系,并证明你的猜想;
②设PQ的长为![]() ,点P的横坐标为m,求
,点P的横坐标为m,求![]() 与m的函数表达式,并求
与m的函数表达式,并求![]() 的最大值;
的最大值;
(3)如果M是抛物线对称轴上一点,在抛物线上是否存在一点N,使得以M、N、C、E为顶点的四边形是平行四边形?若存在,直接写出N点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.

(1)求证:△ADE≌△ABF;
(2)填空:△ABF可以由△ADE绕旋转中心 点,按顺时针方向旋转 度得到;
(3)若BC=8,DE=6,求△AEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB=m(m为常数),点C为直线AB上一点,点P、Q分别在线段BC、AC上,且满足CQ=2AQ,CP=2BP.
![]()
(1)如图,若AB=6,当点C恰好在线段AB中点时,则PQ= ;
(2)若点C为直线AB上任一点,则PQ长度是否为常数?若是,请求出这个常数;若不是,请说明理由;
(3)若点C在点A左侧,同时点P在线段AB上(不与端点重合),请判断2AP+CQ﹣2PQ与1的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高速铁路(简称高铁),是指通过改造原有线路(直线化、轨距标准化),使最高营运速度达到不小于每小时200千米,或者专门修建新的“高速新线”,使营运速率达到每小时250公里以上的铁路系统。宜春距离上海960千米,据了解高铁的平均速度比动车的平均速度每小时快96千米,从上海到宜春坐动车需要的时间是坐高铁需要时间的1.8倍。
(1)根据上面信息,请你求出上海到宜春高铁和动车的平均速度。
(2)广州距北京1800千米,以这样的平均速度坐高铁从广州到北京需要多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年,随着电子商务的快速发展,“电商包裹件”占“快递件”总量的比例逐年增长,根据企业财报,某网站得到如下统计表:
年份 | 2014 | 2015 | 2016 | 2017(预计) |
快递件总量(亿件) | 140 | 207 | 310 | 450 |
电商包裹件(亿件) | 98 | 153 | 235 | 351 |
(1)请选择适当的统计图,描述2014﹣2017年“电商包裹件”占当年“快递件”总量的百分比(精确到1%);
(2)若2018年“快递件”总量将达到675亿件,请估计其中“电商包裹件”约为多少亿件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com