
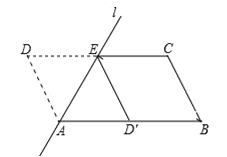
【题目】(2016新疆)如图,ABCD中,AB=2,AD=1,∠ADC=60°,将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕交CD边于点E.
(1)求证:四边形BCED′是菱形;
(2)若点P时直线l上的一个动点,请计算PD′+PB的最小值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题(1)利用翻折变换的性质以及平行线的性质得出∠DAE=∠EAD′=∠DEA=∠D′EA,进而利用平行四边形的判定方法得出四边形DAD′E是平行四边形,进而求出四边形BCED′是平行四边形,根据折叠的性质得到AD=AD′,然后又菱形的判定定理即可得到结论;(2)由四边形DAD′E是平行四边形,得到DAD′E是菱形,推出D与D′关于AE对称,连接BD交AE于P,则BD的长即为PD′+PB的最小值,过D作DG⊥BA于G,解直角三角形得到AG=![]() ,DG=
,DG=![]() ,根据勾股定理即可得到结论.
,根据勾股定理即可得到结论.
试题解析:(1)证明:∵将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,
∴∠DAE=∠D′AE,∠DEA=∠D′EA,∠D=∠AD′E,
∵DE∥AD′,
∴∠DEA=∠EAD′,
∴∠DAE=∠EAD′=∠DEA=∠D′EA,
∴∠DAD′=∠DED′,
∴四边形DAD′E是平行四边形,
∴DE=AD′,
∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC,
∴CE=D′B,CE∥D′B,
∴四边形BCED′是平行四边形;
∵AD=AD′,
∴DAD′E是菱形,
(2)∵四边形DAD′E是菱形,
∴D与D′关于AE对称,
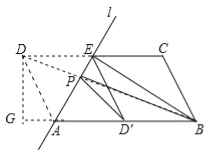
连接BD交AE于P,则BD的长即为PD′+PB的最小值,
过D作DG⊥BA于G,
∵CD∥AB,
∴∠DAG=∠CDA=60°,
∵AD=1,
∴AG=![]() ,DG=
,DG=![]() ,
,
∴BG=![]() ,
,
∴BD=![]() =
=![]() ,
,
∴PD′+PB的最小值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某工厂生产的某种产品按质量分为![]() 个档次,生产第一档次(即最低档次)的产品一天生产
个档次,生产第一档次(即最低档次)的产品一天生产![]() 件,每件利润
件,每件利润![]() 元,每提高一个档次,利润每件增加
元,每提高一个档次,利润每件增加![]() 元.
元.
(1)每件利润为![]() 元时,此产品质量在第几档次?
元时,此产品质量在第几档次?
(2)由于生产工序不同,此产品每提高一个档次,一天产量减少![]() 件.若生产第
件.若生产第![]() 档的产品一天的总利润为
档的产品一天的总利润为![]() 元(其中
元(其中![]() 为正整数,且
为正整数,且![]() ≤
≤![]() ≤
≤![]() ),求出
),求出![]() 关于
关于![]() 的函数关系式;若生产某档次产品一天的总利润为
的函数关系式;若生产某档次产品一天的总利润为![]() 元,该工厂生产的是第几档次的产品?
元,该工厂生产的是第几档次的产品?
查看答案和解析>>
科目:初中数学 来源: 题型:
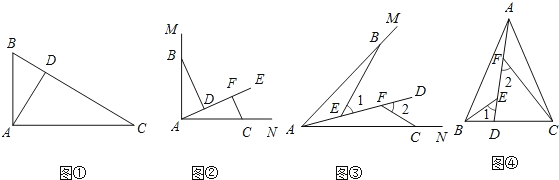
【题目】问题情境:如图①,在直角三角形ABC中,∠BAC=90,AD⊥BC于点D,可知:∠BAD=∠C(不需要证明);
(1)特例探究:如图②,∠MAN=90,射线AE在这个角的内部,点B.C在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.证明:△ABD≌△CAF;
(2)归纳证明:如图③,点B,C在∠MAN的边AM、AN上,点E,F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF;
(3)拓展应用:如图④,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E.F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为18,求△ACF与△BDE的面积之和是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
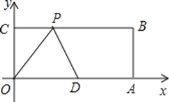
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() 、
、![]() 的坐标为
的坐标为![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 边上运动,当
边上运动,当![]() 是以腰长为5的等腰三角形时,点
是以腰长为5的等腰三角形时,点![]() 的坐标为________________.
的坐标为________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图Rt![]() 中,∠A=30°,OB=2,如果将Rt
中,∠A=30°,OB=2,如果将Rt![]() 在坐标平面内,绕原点O按顺时针方向旋转到
在坐标平面内,绕原点O按顺时针方向旋转到![]() 的位置.
的位置.
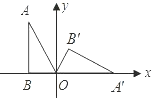
(1)求点![]() 的坐标.
的坐标.
(2)求顶点A从开始到![]() 点结束经过的路径长.
点结束经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
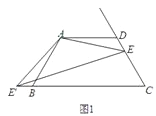
【题目】已知:四边形ABCD中,AD∥BC,AD=AB=CD,∠BAD=120°,点E是射线CD上的一个动点(与C、D不重合),将△ADE绕点A顺时针旋转120°后,得到△ABE',连接EE'.
(1)如图1,∠AEE'= °;
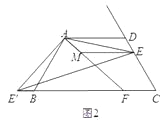
(2)如图2,如果将直线AE绕点A顺时针旋转30°后交直线BC于点F,过点E作EM∥AD交直线AF于点M,写出线段DE、BF、ME之间的数量关系;
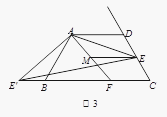
(3)如图3,在(2)的条件下,如果CE=2,AE=![]() ,求ME的长.
,求ME的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com