
把二次函数的表达式y=x2﹣4x+6化为y=a(x﹣h)2+k的形式,那么h+k= .
科目:初中数学 来源: 题型:
密苏里州圣路易斯拱门是座雄伟壮观的抛物线形的建筑物,是美国最高的独自挺立的纪念碑,如图.拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,求拱门的最大高度.



查看答案和解析>>
科目:初中数学 来源: 题型:
在等腰Rt△ABC中,∠BAC=90°,AB=AC,在△ABC外作∠ACM=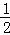 ∠ABC,点D为直线BC上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.
∠ABC,点D为直线BC上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.
(1)当点D在线段BC上时,如图1所示,①∠EDC= 22.5 °;
②探究线段DF与EC的数量关系,并证明;
(2)当点D运动到CB延长线上时,请你画出图形,并证明此时DF与EC的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,为了测量某棵树的高度,小明用长为2m的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点.此时,竹竿与这一点距离相距6m,与树相距15m,则树的高度是( )
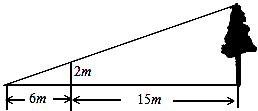
A.7m B.6m C.5m D.4m
查看答案和解析>>
科目:初中数学 来源: 题型:
(1)抛物线m1:y1=a1x2+b1x+c1中,函数y1与自变量x之间的部分对应值如表:
| x | … | ﹣2 | ﹣1 | 1 | 2 | 4 | 5 | … |
| y1 | … | ﹣5 | 0 | 4 | 3 | ﹣5 | ﹣12 | … |
设抛物线m1的顶点为P,与y轴的交点为C,则点P的坐标为 ,点C的坐标为 .
(2)将设抛物线m1沿x轴翻折,得到抛物线m2:y2=a2x2+b2x+c2,则当x=﹣3时,y2= .
(3)在(1)的条件下,将抛物线m1沿水平方向平移,得到抛物线m3.设抛物线m1与x轴交于A,B两点(点A在点B的左侧),抛物线m3与x轴交于M,N两点(点M在点N的左侧).过点C作平行于x轴的直线,交抛物线m3于点K.问:是否存在以A,C,K,M为顶点的四边形是菱形的情形?若存在,请求出点K的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com