
在等腰Rt△ABC中,∠BAC=90°,AB=AC,在△ABC外作∠ACM=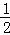 ∠ABC,点D为直线BC上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.
∠ABC,点D为直线BC上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.
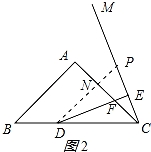
(1)当点D在线段BC上时,如图1所示,①∠EDC= 22.5 °;
②探究线段DF与EC的数量关系,并证明;
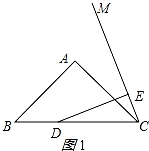
(2)当点D运动到CB延长线上时,请你画出图形,并证明此时DF与EC的数量关系.

【考点】全等三角形的判定与性质;等腰直角三角形.
【分析】(1)①由等腰直角三角形的性质得出∠ABC=∠ACB=4 5°,求出∠BCM=67.5°,即可得出∠EDC的度数;
5°,求出∠BCM=67.5°,即可得出∠EDC的度数;
②作∠PDE=22.5,交CE的延长线于P点,交CA的延长线于N,证明PD=CD,得出PC=2CE,由ASA证明△DNF≌△PNC,得出DF=PC,即可得出结论;
(2)作∠PDE=22.5,交CE的延长线于P点,交CA的延长线于N,证明PD=CD,得出PC=2CE,由ASA证明△DNF≌△PNC,得出DF=PC,即可得出结论.
【解答】(1)①解:如图1所示:
∵∠BAC=90 °,AB=AC,
°,AB=AC,
∴∠ABC=∠ACB=45°,
∵∠ACM=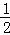 ∠ABC=22.5°,
∠ABC=22.5°,
∴∠BCM=67.5°,
∵DE⊥CM,
∴∠EDC=90°﹣∠BCM=22.5°;
故答案为:22.5;
②DF=2CE.理由如下:
证明:作∠PDE=22.5,交CE的延长线于P点,交CA的延长线于N,如图2所示:
∵DE⊥PC,∠ECD=67.5,
∴∠EDC=22.5°,
∴∠PDE=∠EDC,∠NDC=45°,
∴∠DPC=67.5°
∴PD=CD,
∴PE=EC,
∴PC=2CE,
∵∠NDC=45°,∠NCD=45°,
∴∠NCD =∠NDC,∠DNC=90°,
=∠NDC,∠DNC=90°,
∴ND=NC且∠DNC=∠PNC,
在△DNF和△PNC中,
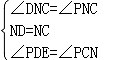 ,
,
∴△DNF≌△PNC(ASA),
∴DF=PC,
∴DF=2CE.
(2)DF=2CE;理由如下:
证明:作∠PDE=22.5,交CE的延长线于P点,交CA的延长线于N,如图3所示:
∵DE⊥PC,∠ECD=67.5,
∴∠EDC=22.5°,
∴∠PDE=∠EDC,∠NDC=45°,
∴∠DPC=67.5°
∴PD=CD,
∴PE=E C,
C,
∴PC=2CE,
∵∠NDC=45°,∠NCD=45°,
∴∠NCD=∠NDC,∠DNC=90°,
∴ND=NC且∠DNC=∠PNC,
在△DNF和△PNC中,
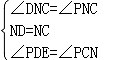 ,
,
∴△DNF≌△PNC(ASA),
∴DF=PC,
∴DF=2CE.

【点评】本题考查了等腰直角三角形的性质与判定、全等三角形的判定与性质、等腰三角形的判定;熟练掌握等腰直角三角形的性质,证明三角形全等是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
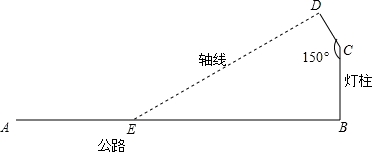
如图,要在宽为28米的公路AB路边安装路灯,路灯的灯臂CD长为3米,且与灯柱BC成150°角,路灯采用圆锥形灯罩,灯罩的轴线DE与灯臂CD垂直,当灯罩的轴线DE能过公路路面的中点时照效果最理想.问应设计多高的灯柱,才能取得最理想的照明效果.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
定义:P、Q分别是两条线段a和b上任意一点,线段PQ的长度的最小值叫做线段a与线段b的距离.
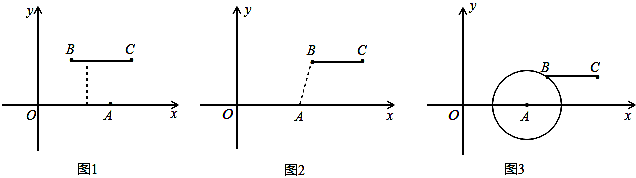
已知O(0,0),A(4,0),B(m,n),C(m+4,n)是平面直角坐标系中四点.
(1)根据上述定义,当m=2,n=2时,如图1,线段BC与线段OA的距离是 ;当m=5,n=2时,如图2,线段BC与线段OA的距离为 ;
(2)如图3,若点B落在圆心为A,半径为2的圆上,线段BC与线段OA的距离记为d,求d关于m的函数解析式.
(3)当m的值变化时,动线段BC与线段OA的距离始终为2,线段BC的中点为M,
①求出点M随线段BC运动所围成的封闭图形的周长;
②点D的坐标为(0,2),m≥0,n≥0,作MH⊥x轴,垂足为H,是否存在m的值使以A、M、H为顶点的三角形与△AOD相似?若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com