
(1)抛物线m1:y1=a1x2+b1x+c1中,函数y1与自变量x之间的部分对应值如表:
| x | … | ﹣2 | ﹣1 | 1 | 2 | 4 | 5 | … |
| y1 | … | ﹣5 | 0 | 4 | 3 | ﹣5 | ﹣12 | … |
设抛物线m1的顶点为P,与y轴的交点为C,则点P的坐标为 ,点C的坐标为 .
(2)将设抛物线m1沿x轴翻折,得到抛物线m2:y2=a2x2+b2x+c2,则当x=﹣3时,y2= .
(3)在(1)的条件下,将抛物线m1沿水平方向平移,得到抛物线m3.设抛物线m1与x轴交于A,B两点(点A在点B的左侧),抛物线m3与x轴交于M,N两点(点M在点N的左侧).过点C作平行于x轴的直线,交抛物线m3于点K.问:是否存在以A,C,K,M为顶点的四边形是菱形的情形?若存在,请求出点K的坐标;若不存在,请说明理由.
【考点】二次函数综合题.
【专题】综合题.
【分析】(1)先利用待定系数法求出抛物线m1的解析式为y1=﹣x2+2x+3,再配成顶点式可得到P点坐标,然后计算自变量为0时的函数值即可得到C点坐标;
(2)根据抛物线的几何变换得到抛物线m1与抛物线m2的二次项系数互为相反数,然后利用顶点式写出抛物线m2的解析式,再计算自变量为﹣3时的函数值;
(3)先确定A点坐标,再根据平移的性质得到四边形AMKC为平行四边形,根据菱形的判定方法,当CA=CK时,四边形AMKC为菱形,接着计算出AC=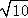 ,则CK=
,则CK=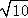 ,然后根据平移的方向不同得到K点坐标.
,然后根据平移的方向不同得到K点坐标.
【解答】解:(1)把(﹣1,0),(1,4),(2,3)分别代入y1=a1x2+b1x+c1得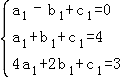 ,
,
解得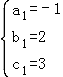 .
.
所以抛物线m1的解析式为y1=﹣x2+2x+3=﹣(x﹣1)2+4,则P(1,4),
当x=0时,y=3,则C(0,3);
(2)因为抛物线m1沿x轴翻折,得到抛物线m2,
所以y2=(x﹣1)2﹣4,当x=﹣3时,y2=(x+1)2﹣4=(﹣3﹣1)2﹣4=12.
故答案为(1,4),(0,3),12;
(3)存在.
当y1=0时,﹣x2+2x+3=0,解得x1=﹣1,x2=3,则A(﹣1,0),B(3,0),
∵抛物线m1沿水平方向平移,得到抛物线m3,
∴CK∥AM,CK=AM,
∴四边形AMKC为平行四边形,
当CA=CK时,四边形AMKC为菱形,而AC=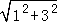 =
=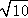 ,则CK=
,则CK=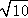 ,
,
当抛物线m1沿水平方向向右平移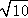 个单位,此时K(
个单位,此时K(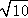 ,3);当抛物线m1沿水平方向向左平移
,3);当抛物线m1沿水平方向向左平移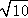 个单位,此时K(﹣
个单位,此时K(﹣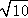 ,3).
,3).
【点评】本题考查了二次函数的综合题:熟练掌握二次函数的性质和菱形的判定;会利用待定系数法求二次函数解析式;会运用数形结合的数学思想方法解决问题.


科目:初中数学 来源: 题型:
定义:P、Q分别是两条线段a和b上任意一点,线段PQ的长度的最小值叫做线段a与线段b的距离.
已知O(0,0),A(4,0),B(m,n),C(m+4,n)是平面直角坐标系中四点.
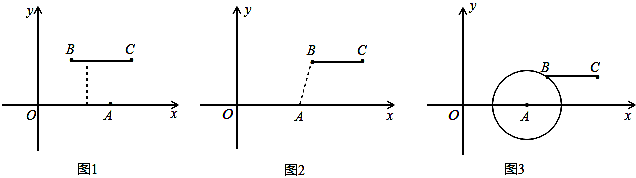
(1)根据上述定义,当m=2,n=2时,如图1,线段BC与线段OA的距离是 ;当m=5,n=2时,如图2,线段BC与线段OA的距离为 ;
(2)如图3,若点B落在圆心为A,半径为2的圆上,线段BC与线段OA的距离记为d,求d关于m的函数解析式.
(3)当m的值变化时,动线段BC与线段OA的距离始终为2,线段BC的中点为M,
①求出点M随线段BC运动所围成的封闭图形的周长;
②点D的坐标为(0,2),m≥0,n≥0,作MH⊥x轴,垂足为H,是否存在m的值使以A、M、H为顶点的三角形与△AOD相似?若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
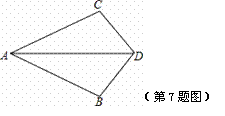
如图,在下列条件中,不能证明△ABD≌△ACD的是
A.BD=DC,AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D.∠B=∠C,BD=DC
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
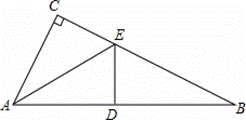
已知:如图,在△ABC中,∠C=90°,AE是△ABC的角平分线;ED平分∠AEB,交AB于点
D;∠CAE∠B.
(1)求∠B的度数.
(2)如果AC=3cm,求AB的长度.
(3)猜想:ED与AB的位置关系,并注明你的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com