
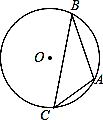
已知:如图,A,B,C为⊙O上的三个点,⊙O的直径为4cm,∠ACB=45°,求AB的长.
科目:初中数学 来源: 题型:
如图,为了测量某棵树的高度,小明用长为2m的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点.此时,竹竿与这一点距离相距6m,与树相距15m,则树的高度是( )
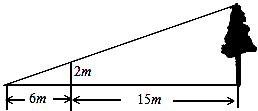
A.7m B.6m C.5m D.4m
查看答案和解析>>
科目:初中数学 来源: 题型:
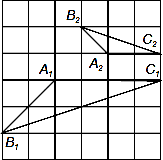
学习相似三角形和解直角三角形的相关内容后,张老师请同学们交流这样的一个问题:“如图,在正方形网格上有△A1B1C1和△A2B2C2,这两个三角形是否相似?”.那么你认为△A1B1C1和△A2B2C2 .(填相似或不相似);理由是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
(1)抛物线m1:y1=a1x2+b1x+c1中,函数y1与自变量x之间的部分对应值如表:
| x | … | ﹣2 | ﹣1 | 1 | 2 | 4 | 5 | … |
| y1 | … | ﹣5 | 0 | 4 | 3 | ﹣5 | ﹣12 | … |
设抛物线m1的顶点为P,与y轴的交点为C,则点P的坐标为 ,点C的坐标为 .
(2)将设抛物线m1沿x轴翻折,得到抛物线m2:y2=a2x2+b2x+c2,则当x=﹣3时,y2= .
(3)在(1)的条件下,将抛物线m1沿水平方向平移,得到抛物线m3.设抛物线m1与x轴交于A,B两点(点A在点B的左侧),抛物线m3与x轴交于M,N两点(点M在点N的左侧).过点C作平行于x轴的直线,交抛物线m3于点K.问:是否存在以A,C,K,M为顶点的四边形是菱形的情形?若存在,请求出点K的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
人体中红细胞的直径约为0.000 007 7 m,用科学记数法表示为
A.7.7×10-5 B.7.7×10-6 C.7.7×10-7 D.77×10-5
查看答案和解析>>
科目:初中数学 来源: 题型:
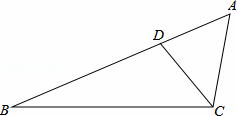
如图,点D在△ABC的AB边上,且∠ACD=∠A.
(1)作∠BDC的平分线DE,交BC于点E(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,判断直线DE与直线AC的位置关系(不要求证明).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com