
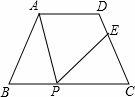
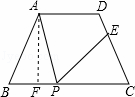
如图,等腰梯形ABCD,AD∥BC,AD=3cm,BC=7cm,∠B=60°,P为下底BC上一点(不与B、C重合),连接AP,过P作∠APE=∠B,交DC于E.
(1)求证:△ABP∽△PCE;
(2)求等腰梯形的腰AB的长;
(3)在底边BC上是否存在一点P,使得DE:EC=5:3?如果存在,求BP的长;如果不存在,请说明理由.
考点: 等腰梯形的性质;解分式方程;三角形的外角性质;相似三角形的判定与性质.
专题: 几何综合题;压轴题.
分析: (1)欲证△ABP∽△PCE,需找出两组对应角相等;由等腰梯形的性质可得出∠B=∠C,根据三角形外角的性质可证得∠EPC=∠BAP;由此得证;
(2)可过作AF⊥BC于F,由等腰梯形的性质得到AF是BC、AD差的一半,在Rt△ABF中,根据∠B的度数及BF的长即可求得AB的值;
(3)在(2)中求得了AB的长,即可求出DE:EC=5:3时,DE、CE的值.设BP的长为x,进而可表示出PC的长,然后根据(1)的相似三角形,可得出关于AB、BP、PC、CE的比例关系式,由此可得出关于x的分式方程,若方程有解,则x的值即为BP的长.若方程无解,则说明不存在符合条件的P点.
解答: (1)证明:由∠APC为△ABP的外角得∠APC=∠B+∠BAP;
∵∠B=∠APE
∴∠EPC=∠BAP
∵∠B=∠C
∴△ABP∽△PCE;
(2)解:过A作AF⊥BC于F;
∵等腰梯形ABCD中,AD=3cm,BC=7cm,
∴BF=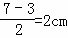 ,
,
∵Rt△ABF中,∠B=60°,BF=2;
∴AB=4cm;
(3)解:存在这样的点P.
理由是:∵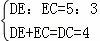
解之得EC=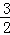 cm.
cm.
设BP=x,则PC=7﹣x
由△ABP∽△PCE可得
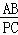 =
=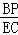 ,
,
∵AB=4,PC=7﹣x,
∴ =
=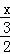
解之得x1=1,x2=6,
经检验都符合题意,
即BP=1cm或BP=6cm.
点评: 此题主要考查了等腰梯形的性质,以及相似三角形的判定和性质.


科目:初中数学 来源: 题型:
观察下列球的排列规律(其中●是实心球,○是空心球):
●○○●●○○○○○●○○●●○○○○○●○○●●○○○○○●…从第1个球起到第2009个球止,共有实心球 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从A点出发到B点止,动点E从C点出发到A点止.点D运动的速度为1cm/秒,点E运动的速度为2cm/秒.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是( )
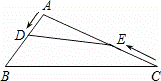
A. 3秒或4.8秒 B. 3秒 C. 4.5秒 D. 4.5秒或4.8秒
查看答案和解析>>
科目:初中数学 来源: 题型:
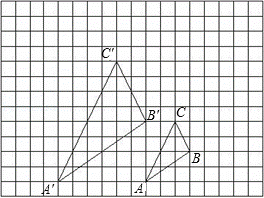
如图,图中小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点O为位似中心的位似图形,它们的顶点都在小正方形顶点上.
(1)画出位似中心点O;
(2)△ABC与△A′B′C′的位似比为 1:2 ;
(3)以点O为位似中心,再画一个△A1B1C1,使它与△ABC的位似为1:2.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,上体育课,九年级三班的甲、乙两名同学分别站在C、D的位置时,乙的影子恰好在甲的影子里边,已知甲,乙同学相距1米.甲身高1.8米,乙身高1.5米,则甲的影长是( )
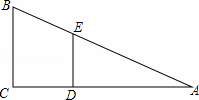
A. 4米 B. 5米 C. 6米 D. 7米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com