
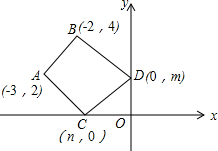
 如图,A(-3,2),B(-2,4),C(n,0),D(0,m),若四边形ABCD的周长最小,求-
如图,A(-3,2),B(-2,4),C(n,0),D(0,m),若四边形ABCD的周长最小,求-| m |
| n |
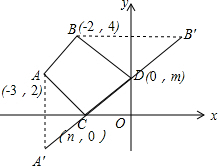 解:∵四边形ABCD周长=AB+BC+CD+AD,AB是定值,
解:∵四边形ABCD周长=AB+BC+CD+AD,AB是定值,
|
|
| 6 |
| 5 |
| 8 |
| 5 |
| 4 |
| 3 |
| 8 |
| 5 |
| 4 |
| 3 |
| 8 |
| 5 |
| m |
| n |
| ||
-
|
| 6 |
| 5 |


科目:初中数学 来源: 题型:
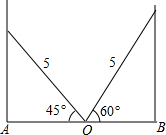 如图,学校的保管室里,有一架5米长的梯子斜靠在墙上,此时梯子与地面所成的角为45°,如果梯子的底端O固定不动,顶端靠在对面墙上,此时梯子与地面所成的角为60°,求此保管室的宽度AB的长.
如图,学校的保管室里,有一架5米长的梯子斜靠在墙上,此时梯子与地面所成的角为45°,如果梯子的底端O固定不动,顶端靠在对面墙上,此时梯子与地面所成的角为60°,求此保管室的宽度AB的长.查看答案和解析>>
科目:初中数学 来源: 题型:
| A、①和② | B、②和③ |
| C、③和④ | D、①和④ |
查看答案和解析>>
科目:初中数学 来源: 题型:
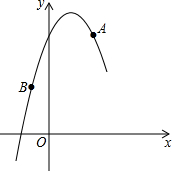 如图,在平面直角坐标系中,抛物线y=ax2+bx+5经过A(2,5),B(-1,2)两点,若点C在该抛物线上,则C点的坐标可能是( )
如图,在平面直角坐标系中,抛物线y=ax2+bx+5经过A(2,5),B(-1,2)两点,若点C在该抛物线上,则C点的坐标可能是( )| A、(-2,0) |
| B、(0.5,6.5) |
| C、(3,2) |
| D、(2,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,时钟的钟面上标有1,2,3…,12共12个数,一条直线把钟面分成了两部分.请你再画一条直线分割钟面,使钟面被分成三个不同的部分且各部分所包含的几个数的和都相等.
如图,时钟的钟面上标有1,2,3…,12共12个数,一条直线把钟面分成了两部分.请你再画一条直线分割钟面,使钟面被分成三个不同的部分且各部分所包含的几个数的和都相等.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com