
提出问题:当x>0时如何求函数y=x+ 的最大值或最小值?
的最大值或最小值?
分析问题:前面我们刚刚学过二次函数的相关知识,知道求二次函数的最值时,我们可以利用它的图象进行猜想最值,或利用配方可以求出它的最值.
例如我们求函数y=x﹣2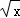 (x>0)的最值时,就可以仿照二次函数利用配方求最值的方法解决问题;y=x﹣2
(x>0)的最值时,就可以仿照二次函数利用配方求最值的方法解决问题;y=x﹣2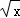 =(
=(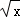 )2﹣2
)2﹣2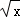 ﹣2
﹣2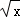 +1﹣1=(
+1﹣1=(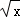 ﹣1)2﹣1即当x=1时,y有最小值为﹣1
﹣1)2﹣1即当x=1时,y有最小值为﹣1
解决问题
借鉴我们已有的研究函数的经验,探索函数y=x+ (x>0)的最大(小)值.
(x>0)的最大(小)值.
(1)实践操作:填写下表,并用描点法画出函数y=x+ (x>0)的图象:
(x>0)的图象:
x | … |
|
|
| 1 | 2 | 3 | 4 | … |
y | … | … |
(2)观察猜想:观察该函数的图象,猜想
当x= 时,函数y=x+ (x>0)有最 值(填“大”或“小”),是 .
(x>0)有最 值(填“大”或“小”),是 .
(3)推理论证:利用上述例题,请你尝试通过配方法求函数y=x+ (x>0)的最大(小)值,以证明你的猜想.知识能力运用:直接写出函数y=﹣2x﹣
(x>0)的最大(小)值,以证明你的猜想.知识能力运用:直接写出函数y=﹣2x﹣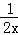 (x>0)当x= 时,该函数有最 值(填“大”或“小”),是 .
(x>0)当x= 时,该函数有最 值(填“大”或“小”),是 .

科目:初中数学 来源:2016届浙江省九年级上学期12月质检数学试卷(解析版) 题型:填空题
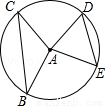
如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD.已知DE=6,∠BAC+∠EAD=180°,则弦BC的弦心距等于 .
查看答案和解析>>
科目:初中数学 来源:2016届江苏省九年级上学期第一次月考数学试卷(解析版) 题型:解答题
已知△ABC中,a、b、c分别为∠A、∠B、∠C的对边,方程cx2+bx﹣a=0是关于x的一元二次方程.
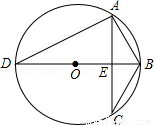
(1)判断方程cx2+bx﹣a=0的根的情况为 (填序号);
①方程有两个相等的实数根;
②方程有两个不相等的实数根;
③方程无实数根;
④无法判断
(2)如图,若△ABC内接于半径为2的⊙O,直径BD⊥AC于点E,且∠D=30°,求方程cx2+bx﹣a=0的根;
(3)若x=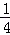 a是方程cx2+bx﹣a=0的一个根,△ABC的三边a、b、c的长均为整数,试求a、b、c的值.
a是方程cx2+bx﹣a=0的一个根,△ABC的三边a、b、c的长均为整数,试求a、b、c的值.
查看答案和解析>>
科目:初中数学 来源:2016届江苏省九年级上学期第一次月考数学试卷(解析版) 题型:填空题
扬州一电信销售中心八月份销售某款手机50部,计划九、十月份共销售132部.设九、十月每月的平均增长率为x,根据题意列出的方程是 .
查看答案和解析>>
科目:初中数学 来源:2016届江苏省九年级上学期第一次月考数学试卷(解析版) 题型:选择题
点A、O、D与点B、O、C分别在同一直线上,图中弦的条数为( )
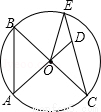
A.2 B.3 C.4 D.5
查看答案和解析>>
科目:初中数学 来源:2016届江苏省九年级上学期第三次段考数学试卷(解析版) 题型:解答题
标有﹣3,﹣2,4的三张不透明的卡片,除正面写有不同的数字外,其余的值都相同,将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记为二次函数解析式y=a(x﹣k)2+b的k值,第二次从余下的两张卡片中再抽取一张,上面标有的数字记为二次函数解析式的b值.
(1)写出k为负数的概率;
(2)求二次函数y=a(x﹣k)2+b的图象上顶点在双曲线y=﹣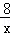 上的概率.(用树状图或列举法求解)
上的概率.(用树状图或列举法求解)
查看答案和解析>>
科目:初中数学 来源:2016届江苏省九年级上学期第三次月考数学试卷(解析版) 题型:解答题
如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上任意一点(不与A,B重合),且CD切⊙O于点D.
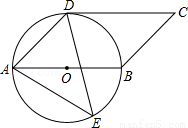
(1)试求∠AED的度数.
(2)若⊙O的半径为 cm,试求:△ADE面积的最大值.
cm,试求:△ADE面积的最大值.
查看答案和解析>>
科目:初中数学 来源:2016届江苏省泰州市九年级上学期第二次月考数学试卷(解析版) 题型:填空题
在一个不透明的口袋中装有若干个只有颜色不同的球,如果已知袋中只有4个红球,且摸出红球的概率为 ,那么袋中的球共有 个.
,那么袋中的球共有 个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com