
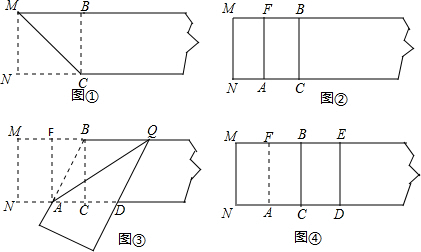
���� ��1������AB�����۵������ʣ��ɵ�AC=2����Rt��ABC�У����ù��ɶ��������AB�ij��ȣ�
��2���������CD=2��ND�����ɻƽ���εĶ��弴�������жϣ�
��3������Q��QH��ND�ڵ�H����tan��QDH=tan��ABM�������DH�ij��ȣ��̶��ó�AH�ij��ȣ���Rt��AHQ�����ù��ɶ������AQ���̶������ù��ɶ����������ֱ��������б�ߵij���
��4����FG��DQ��G����AQ��S����ST��FQ��T����ͼ�ۣ����۵������ʵá�BQA=��DQA�����ݽ�ƽ�������ʵ�ST=SG����FG=ST+SF�����ô��߶���̿��ж�FS+ST����СֵΪFG�ij���Ȼ��֤��Rt��QDH��Rt��FQG�����������Ʊȼ���FG���ɣ�
��� �⣺��1�����ı���MNCB�������Σ�
��NC=MN=4cm��
���۵������ʵã�AC=$\frac{1}{2}$NC=2cm��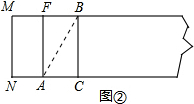 ����AB����ͼ�ڣ�
����AB����ͼ�ڣ�
��Rt��ABC��AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$��
�ʴ�Ϊ2$\sqrt{5}$��
��2��ͼ���еĻƽ�����У�����BCDE������MNDE��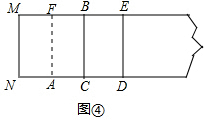 ��AD=2$\sqrt{5}$��AN=AC=2��
��AD=2$\sqrt{5}$��AN=AC=2��
��CD=2$\sqrt{5}$-2��ND=2$\sqrt{5}$+2��
��$\frac{CD}{BC}$=$\frac{2\sqrt{5}-2}{4}$=$\frac{\sqrt{5}-1}{2}$��
�ʾ���BCDE�ǻƽ���Σ�
��$\frac{MN}{ND}$=$\frac{4}{2\sqrt{5}+2}$=$\frac{\sqrt{5}-1}{2}$��
�ʾ���MNDE�ǻƽ���Σ�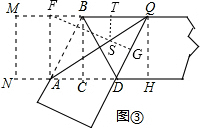 ��3������Q��QH��ND�ڵ�H����ͼ����ʾ��
��3������Q��QH��ND�ڵ�H����ͼ����ʾ��
���۵������ʿɵã���ADQ=��ABQ��
���QDH=��ABM��
��tan��QDH=tan��ABM=$\frac{4}{2}$=$\frac{QH}{DH}$=$\frac{4}{DH}$��
��DH=2��
��AH=AD+DH=2$\sqrt{5}$+2��
��Rt��AQH��AQ2=AH2+QH2=��2$\sqrt{5}$+2��2+16=40+8$\sqrt{5}$��
BD2=CD2+BC2=��2$\sqrt{5}$-2��2+16=40-8$\sqrt{5}$��
��AQ��BDΪ��ֱ�DZ���ֱ�������Σ����ֱ��������б�߳�=$\sqrt{A{Q}^{2}+B{D}^{2}}$=$\sqrt{80}$=4$\sqrt{5}$��
��4����FG��DQ��G����AQ��S����ST��FQ��T����ͼ�ۣ�
���۵������ʵá�BQA=��DQA��
��ST=SG��
��FG=ST+SF��
��FS+ST����СֵΪFG�ij���
�ߡ�QDH=��FQD��
��Rt��QDH��Rt��FQG��
��$\frac{QH}{FG}$=$\frac{DQ}{FQ}$����$\frac{4}{FG}$=$\frac{2\sqrt{5}}{2+2\sqrt{5}}$��
��FG=$\frac{20+4\sqrt{5}}{5}$��
��FS+ST����СֵΪ$\frac{20+4\sqrt{5}}{5}$��
���� ���⿼���˼��α任���ۺϣ��漰���۵������ʡ����ɶ�����������Ǻ����Ķ��壬�ۺϿ����֪ʶ��϶࣬�������Ҫ���Ǿ�����ʵ�Ļ����������ν�ϣ������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | xy4 | B�� | xy5 | C�� | x+y4 | D�� | x+y5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3-2=-9 | B�� | ��72��3=75 | C�� | x10��x5=x2 | D�� | $\frac{1}{\sqrt{2}-1}$=$\sqrt{2}$+1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
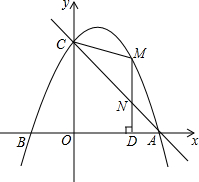 ��ͼ�����κ���y=-$\frac{1}{2}$x2+bx+c��ͼ����A��B��-2��0����C��0��4������ֱ��AC����M�Ƕ��κ���ͼ���ϵ�һ���㣬������MD��x�ᣬ����Ϊ��D����ֱ��AC�ڵ�N������CM��
��ͼ�����κ���y=-$\frac{1}{2}$x2+bx+c��ͼ����A��B��-2��0����C��0��4������ֱ��AC����M�Ƕ��κ���ͼ���ϵ�һ���㣬������MD��x�ᣬ����Ϊ��D����ֱ��AC�ڵ�N������CM���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
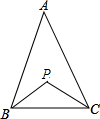 ��ͼ���ڡ�ABC�У�BP��CP�ֱ�Ϊ��B����C��ƽ���ߣ���̽����A�͡�P֮�����������������ϵ��˵˵������ɣ�
��ͼ���ڡ�ABC�У�BP��CP�ֱ�Ϊ��B����C��ƽ���ߣ���̽����A�͡�P֮�����������������ϵ��˵˵������ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABC�У���BAC=60�㣬��ABC=45�㣬AB=$\sqrt{2}$��D���߶�BC�ϵ�һ�����㣬��ADΪֱ������O�ֱ�AB��AC��E��F������EF�����߶�EF���ȵ���СֵΪ$\frac{\sqrt{3}}{2}$��
��ͼ����ABC�У���BAC=60�㣬��ABC=45�㣬AB=$\sqrt{2}$��D���߶�BC�ϵ�һ�����㣬��ADΪֱ������O�ֱ�AB��AC��E��F������EF�����߶�EF���ȵ���СֵΪ$\frac{\sqrt{3}}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
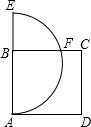 ��ͼ��������ABCD�ı߳�����3����E��AB�ӳ�����һ�㣬��AE=5����AEΪֱ���İ�Բ��BC�ڵ�F����BF=$\sqrt{6}$��
��ͼ��������ABCD�ı߳�����3����E��AB�ӳ�����һ�㣬��AE=5����AEΪֱ���İ�Բ��BC�ڵ�F����BF=$\sqrt{6}$���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com