
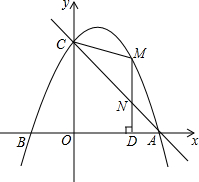
 ��ͼ�����κ���y=-$\frac{1}{2}$x2+bx+c��ͼ����A��B��-2��0����C��0��4������ֱ��AC����M�Ƕ��κ���ͼ���ϵ�һ���㣬������MD��x�ᣬ����Ϊ��D����ֱ��AC�ڵ�N������CM��
��ͼ�����κ���y=-$\frac{1}{2}$x2+bx+c��ͼ����A��B��-2��0����C��0��4������ֱ��AC����M�Ƕ��κ���ͼ���ϵ�һ���㣬������MD��x�ᣬ����Ϊ��D����ֱ��AC�ڵ�N������CM������ ��1������B��-2��0����C��0��4���ֱ����y=-$\frac{1}{2}$x2+bx+c�У��г�b��c�Ķ�Ԫһ�η����飬���b��c��ֵ���ɣ�
��2�����ı���OCMDΪ���Σ����MCO=��CMD=90�㣬OC=MD�����ǵõ�-$\frac{1}{2}$x2+x+4=4�����x��ֵ���ɣ�
��3����ֱ��AC�ĺ�������ʽΪy=kx+b����y=0����-$\frac{1}{2}$x2+x+4=0�������A�����꣬�������ֱ��AC�ĺ�������ʽ����M��N���Ϸ����·������m��ȡֵ��Χ��д��m��d�ĺ�����ϵʽ��
��4�����������������OE�ij���Ȼ��ֵ�M�ڵ�N���Ϸ�ʱ���·�ʱ����MN=2�����m��ֵ���ɣ�
��� �⣺��1������B��-2��0����C��0��4���ֱ����y=-$\frac{1}{2}$x2+bx+c�У�
��$\left\{\begin{array}{l}{-\frac{1}{2}��4-2b+c=0}\\{c=4}\end{array}\right.$���$\left\{\begin{array}{l}{b=1}\\{c=4}\end{array}\right.$��
��������κ�������ʽΪy=-$\frac{1}{2}$x2+x+4��
��2�����ı���OCMDΪ���Σ����MCO=��CMD=90�㣬OC=MD��
��-$\frac{1}{2}$x2+x+4=4��
���x1=0��x2=2��
���M������2��4����
��3����y=0����-$\frac{1}{2}$x2+x+4=0��
���x1=-2��x2=4�����A������4��0����
��ֱ��AC�ĺ�������ʽΪy=kx+b��
�����⣬��$\left\{\begin{array}{l}{4k+b=0}\\{b=4}\end{array}\right.$���$\left\{\begin{array}{l}{k=-1}\\{b=4}\end{array}\right.$��
ֱ��AC�ĺ�������ʽΪy=-x+4��
�ߵ�M�ĺ�����Ϊm��
���M��������m��-$\frac{1}{2}$x2+x+4����
��N��������m��-m+4����
��M��N���Ϸ�����0��m��4ʱ��d=-$\frac{1}{2}$m2+m+4-��-m+4��=-$\frac{1}{2}$m2+2m��
��M��N���·�����m��0��m��4ʱd=��-m+4��-��-$\frac{1}{2}$m2+m+4��=$\frac{1}{2}$m2-2m��
����d=$\left\{\begin{array}{l}{-\frac{1}{2}{m}^{2}+2m��0��m��4��}\\{\frac{1}{2}{m}^{2}-2m��m��0��m��4��}\end{array}\right.$��
��4���ߵ�E��OC���е㣬��C������Ϊ��0��4����
��OE=2��
�ٵ���M�ڵ�N���Ϸ�ʱ��MN=-$\frac{1}{2}$m2+2m=2��
���m1=m2=2��
��m=2��
�ڵ���M�ڵ�N���·�ʱ��MN=$\frac{1}{2}$m2-2m=2��
���m1=2-2$\sqrt{2}$��m2=2+2$\sqrt{2}$��
��m=2-2$\sqrt{2}$��m=2+2$\sqrt{2}$��
�ۺ����������Ե�M��N��E��CΪ������ı�����ƽ���ı���ʱ��
m��ֵΪm1=2��m2=2-2$\sqrt{2}$��m3=2+2$\sqrt{2}$��
���� ������Ҫ�����˶��κ������ۺ��⣬�����漰������ϵ��������κ����Ľ���ʽ�����ε����ʡ�ƽ���ı��ε��ж���֪ʶ�������Ĺؼ��Ƕ�M��N��λ�÷������ۣ�����������ʶ���Ҫ���з������ۣ�������һ�����Ѷȣ�


 �����ܿ����ϵ�д�
�����ܿ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
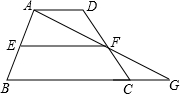 ����ABCD�У�AD��BC��E��F�ֱ���AB��CD���е㣬����AF���ӳ���BC�ӳ����ڵ�G��
����ABCD�У�AD��BC��E��F�ֱ���AB��CD���е㣬����AF���ӳ���BC�ӳ����ڵ�G���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
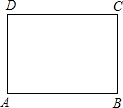 ��ͼ����һ�ų�Ϊ9cm����Ϊ8cm�ľ���ֽƬ�ϣ���Ҫ����һ������Ϊ5cm�Ķ۽ǵ��������Σ�����µĶ۽ǵ������������ϵĸ�Ϊ3��4cm����Ҫ�۽ǵ��������ε�һ����������ε�һ�������غϣ��������������ھ��εı��ϣ�
��ͼ����һ�ų�Ϊ9cm����Ϊ8cm�ľ���ֽƬ�ϣ���Ҫ����һ������Ϊ5cm�Ķ۽ǵ��������Σ�����µĶ۽ǵ������������ϵĸ�Ϊ3��4cm����Ҫ�۽ǵ��������ε�һ����������ε�һ�������غϣ��������������ھ��εı��ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����һ�������� | |
| B�� | �ڰ��д�5�Ѳ�ͬ��Կ������������һ�ѣ����������� | |
| C�� | ���ӻ�����ѡһ��Ƶ������Ļ�����ڲ����������� | |
| D�� | ������������������6���飬��������һ���������������� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com