
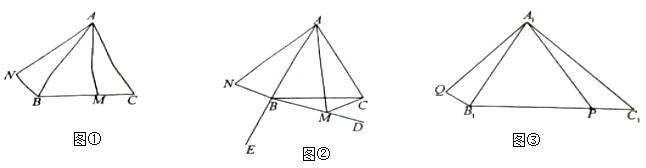
【题目】(1)在![]() 中,
中,![]() ,
,![]() 是平面内任意一点,将线段
是平面内任意一点,将线段![]() 绕点
绕点![]() 顺时针旋转与
顺时针旋转与![]() 相等的角度,得到线段
相等的角度,得到线段![]() ,连接
,连接![]() .
.
①如图①,若![]() 是线段
是线段![]() 上的一点,且
上的一点,且![]() ,
,![]() ,则
,则![]() 的大小
的大小![]() (度),
(度),![]() 的长
的长![]() ;
;
②如图②,点![]() 是
是![]() 延长线上的一点,若
延长线上的一点,若![]() 是
是![]() 内部射线
内部射线![]() 上任意一点,连接
上任意一点,连接![]() ,
,![]() 与
与![]() 的数量关系是什么?
的数量关系是什么?![]() 与
与![]() 的数量关系是什么?并分别给予证明:
的数量关系是什么?并分别给予证明:
(2)如图③,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上的任意一点,连接
上的任意一点,连接![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到线段
,得到线段![]() ,连接
,连接![]() ,求线段
,求线段![]() 长度的最小值(直接写出结果即可).
长度的最小值(直接写出结果即可).
【答案】(1)①![]() , 2;②
, 2;②![]() ,
,![]() ;证明见解析;(2)
;证明见解析;(2)![]()
【解析】
(1)①根据旋转的性质可得∠NAM=∠BAC,AN=AM,然后可得∠NAB=∠MAC=20°,再利用SAS证明![]() 即可得到NB=MC=2;
即可得到NB=MC=2;
②同①证明![]() 即可;
即可;
(2)如图③,在A1C1上截取A1N=A1B1,连接PN,作NH⊥B1C1于H,作A1M⊥B1C1于M,利用全等三角形的判定和性质证明B1Q=PN,推出当PN的值最小时, B1Q的值最小,解直角三角形求出NH的值即可解决问题.
解:(1)①由题意可得:∠NAM=∠BAC,
∴∠NAM-∠BAM =∠BAC-∠BAM,即∠NAB=∠MAC=20°,
又∵AN=AM,AB=AC,
∴![]() ,
,
∴NB=MC=2,
故答案为:20,2;
②![]() ,
,![]() ;
;
证明:![]() 将线段
将线段![]() 绕点
绕点![]() 顺时针旋转与
顺时针旋转与![]() 相等的角度,得到线段
相等的角度,得到线段![]() ,
,
![]() ,
,
∴∠NAM-∠BAM =∠BAC-∠BAM,
![]() ,
,
在![]() 和
和![]() 中,
中,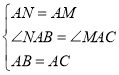 ,
,
![]() ,
,
![]() ;
;
(2)如图③,在A1C1上截取A1N=A1B1,连接PN,作NH⊥B1C1于H,作A1M⊥B1C1于M.
∵∠C1A1B1=∠PA1Q,
∴∠QA1B1=∠PA1N,
∵A1Q=A1P,A1B1=A1N,
∴△QA1B1≌△PA1N(SAS),
∴B1Q=PN,
∴当PN的值最小时, B1Q的值最小,
在Rt△A1B1M中,
∵∠A1B1M=60°,A1B1=8,
∴A1M=A1B1sin60°=![]() ,
,
∵∠MA1C1=∠B1A1C1∠B1A1M=75°30°=45°,
∴A1C1=![]() ,
,
∴NC1=A1C1A1N=![]() ,
,
在Rt△NHC1,
∵∠C1=45°,
∴NH=![]() ,
,
根据垂线段最短可知,当点P与H重合时,PN的值最小,
∴B1Q的最小值为![]() .
.


科目:初中数学 来源: 题型:
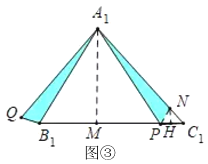
【题目】阅读下面材料:
定义:与圆的所有切线和割线都有公共点的几何图形叫做这个圆的关联图形.
问题:⊙O的半径为1,画一个⊙O的关联图形.
在解决这个问题时,小明以O为原点建立平面直角坐标系xOy进行探究,他发现能画出很多⊙O的关联图形,例如:⊙O本身和图1中的△ABC(它们都是封闭的图形),以及图2中以O为圆心的![]() (它是非封闭的形),它们都是⊙O的关联图形.而图2中以P,Q为端点的一条曲线就不是⊙O的关联图形.
(它是非封闭的形),它们都是⊙O的关联图形.而图2中以P,Q为端点的一条曲线就不是⊙O的关联图形.
参考小明的发现,解决问题:
(1)在下列几何图形中,①⊙O的外切正多边形;②⊙O的内接正多边形;③⊙O的一个半径大于1的同心圆;⊙O的关联图形是______(填序号).
(2)若图形G是⊙O的关联图形,并且它是封闭的,则图形G的周长的最小值是____.
(3)在图2中,当⊙O的关联图形![]() 的弧长最小时,经过D,E两点的直线为y=____.
的弧长最小时,经过D,E两点的直线为y=____.
(4)请你在备用图中画出一个⊙O的关联图形,所画图形的长度l小于(2)中图形G的周长的最小值,并写出l的值(直接画出图形,不写作法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,图中的小方格都是边长为1的正方形,△ABC与△A'B'C'是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
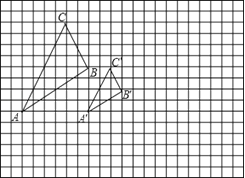
(1)画出位似中心点O;
(2)直接写出△ABC与△A′B′C′的位似比_______
(3)以位似中心O为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,画出△A′B′C′关于点O中心对称的△A″B″C″,并直接写出△A″B″C″各顶点的坐标._______;_______;_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 中(
中(![]() ,
,![]() 是常数)的自变量
是常数)的自变量![]() 与函数值
与函数值![]() 的部分对应值如下表:
的部分对应值如下表:
| …… |
| 0 | 1 | 2 | 3 | 4 | …… |
| …… | 10 | 5 | 2 | 1 | 2 | 5 | …… |
下列结论正确的是:
A.当![]() 时,
时,![]() 有最大值1
有最大值1
B.当![]() 时,
时,![]() 随
随![]() 的增大而增大
的增大而增大
C.点![]() 在该函数的图像上
在该函数的图像上
D.若![]() ,
,![]() 两点都在该函数的图象上,则当
两点都在该函数的图象上,则当![]() 时,
时,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
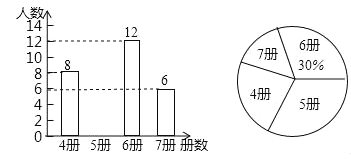
【题目】高尔基说:“书,是人类进步的阶梯.”阅读可以丰富知识、拓展视野、充实生活等诸多益处.为了解学生的课外阅读情况,某校随机抽查了部分学生阅读课外书册数的情况,并绘制出如下统计图,其中条形统计图因为破损丢失了阅读5册书数的数据.
(1)求条形图中丢失的数据,并写出阅读书册数的众数和中位数;
(2)根据随机抽查的这个结果,请估计该校1200名学生中课外阅读5册书的学生人数;
(3)若学校又补查了部分同学的课外阅读情况,得知这部分同学中课外阅读最少的是6册,将补查的情况与之前的数据合并后发现中位数并没有改变,试求最多补查了多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
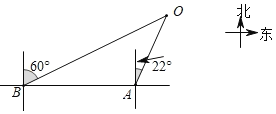
【题目】2019年4月23日是中国人民解放军海军成立70周年纪念日,届时将在青岛举行盛大的多国海军庆祝活动.为此我国海军进行了多次军事演习.如图,在某次军事演习时,舰艇A发现在他北偏东22°方向上有不明敌舰在指挥中心O附近徘徊,快速报告给指挥中心,此时在舰艇A正西方向50海里处的舰艇B接到返回指挥中心的行动指令,舰艇B迅速赶往在他北偏东60°方向的指挥中心处,舰艇B的速度是80海里/小时,请根据以上信息,求舰艇B到达指挥中心O的时间.(结果精确到0.1小时,参考数据:(sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,![]() =1.73)
=1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
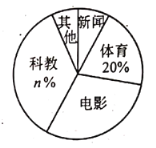
【题目】学校为了解全校![]() 名学生双休日在家最爱选择的电视频道情况,问卷要求每名学生从“新闻,体育,电影,科教,其他”五项中选择其一,随机抽取了部分学生,调查结果绘制成未完成的统计图表如下:
名学生双休日在家最爱选择的电视频道情况,问卷要求每名学生从“新闻,体育,电影,科教,其他”五项中选择其一,随机抽取了部分学生,调查结果绘制成未完成的统计图表如下:
频道 | 新闻 | 体育 | 电影 | 科教 | 其他 |
人数 |
|
|
|
|
|
![]() 求调查的学生人数及统计图表中
求调查的学生人数及统计图表中![]() 的值;
的值;
![]() 求选择其他频道在统计图中对应扇形的圆心角的度数;
求选择其他频道在统计图中对应扇形的圆心角的度数;
![]() 求全校最爱选择电影频道的学生人数.
求全校最爱选择电影频道的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为5,点A、B、C都在⊙O上,∠CAB的平分线交⊙O于点D.
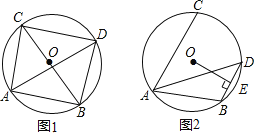
(1)如图1,若BC为⊙O的直径,AB=6,求AC和BD的长;
(2)如图2,若∠CAB=60°,过圆心O作OE⊥BD于点E,求OE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com