
【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别为AB , AC边上的中点,连接DE , 将△ADE绕点E旋转180°得到△CFE , 连接AF , AC . 求证:四边形ADCF是菱形;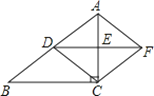
【答案】解答:证明:∵将△ADE绕点E旋转180°得到△CFE ,
∴AE=CE , DE=EF ,
∴四边形ADCF是平行四边形,
∵D、E分别为AB , AC边上的中点,
∴DE是△ABC的中位线,
∴DE∥BC ,
∵∠ACB=90°,
∴∠AED=90°,
∴DF⊥AC ,
∴四边形ADCF是菱形.
【解析】根据旋转可得AE=CE , DE=EF , 可判定四边形ADCF是平行四边形,然后证明DF⊥AC , 可得四边形ADCF是菱形.
【考点精析】通过灵活运用三角形中位线定理和菱形的判定方法,掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形即可以解答此题.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】下列变形属于移项的是( )
A. 由3x+2-2x=5,得3x-2x+2=5
B. 由3x+2x=1,得5x=1
C. 由2(x-1)=3,得2x-2=3
D. 由9x+5=-3,得9x=-3-5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,过对角线BD上任一点P , 作EF∥BC , GH∥AB , 下列结论正确的是 . (填序号)
①图中共有3个菱形;
②△BEP≌△BGP;
③四边形AEPH的面积等于△ABD的面积的一半;
④四边形AEPH的周长等于四边形GPFC的周长.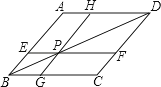
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD的边长2,∠A=60°,点E、F分别在边AB、AD上,若将△AEF沿直线EF折叠,使得点A恰好落在CD边的中点G处,则EF= .

查看答案和解析>>
科目:初中数学 来源: 题型:
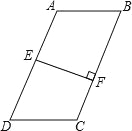
【题目】如图,在四边形ABCD中,AB∥DC,E是AD中点,EF⊥BC于点F,BC=5,EF=3.
(1)若AB=DC,则四边形ABCD的面积S= ;
(2)若AB>DC,则此时四边形ABCD的面积S′ S(用“>”或“=”或“<”填空).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com