
分析 原式分母有理化化简得到结果,把a与b的值代入计算即可求出值.
解答 解:原式=$\frac{2ab(a\sqrt{b}-b\sqrt{a})}{{a}^{2}b-{ab}^{2}}$+$\frac{(a+b)(\sqrt{a}-\sqrt{b})}{a-b}$
=$\frac{2a\sqrt{b}-2b\sqrt{a}+a\sqrt{a}-a\sqrt{b}+b\sqrt{a}-b\sqrt{b}}{a-b}$
=$\frac{(a-b)\sqrt{b}+(a-b)\sqrt{a}}{a-b}$
=$\sqrt{a}$+$\sqrt{b}$,
当a=20,b=45时,原式=$\sqrt{20}$+$\sqrt{45}$=2$\sqrt{5}$+3$\sqrt{5}$=5$\sqrt{5}$.
点评 此题考查了二次根式的化简求值,熟练掌握运算法则是解本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 将抛物线C向右平移$\frac{5}{2}$个单位 | B. | 将抛物线C向右平移3个单位 | ||
| C. | 将抛物线C向右平移5个单位 | D. | 将抛物线C向右平移6个单位 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
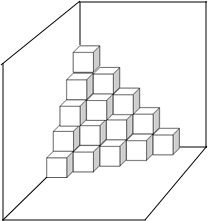 如图,是按规律摆放在墙角的一些小正方体,从上往下分别记为第一层,第二层,第三层…第n层.
如图,是按规律摆放在墙角的一些小正方体,从上往下分别记为第一层,第二层,第三层…第n层.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$R2 | B. | πR2 | C. | $\frac{3\sqrt{3}}{2}$R2 | D. | $\frac{3\sqrt{3}}{4}$R2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
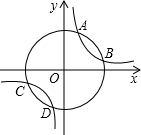 如图,以原点为圆心的圆与反比例函数y=$\frac{3}{x}$的图象交于A、B、C、D四点,已知点A的横坐标为1,则点C的横坐标( )
如图,以原点为圆心的圆与反比例函数y=$\frac{3}{x}$的图象交于A、B、C、D四点,已知点A的横坐标为1,则点C的横坐标( )| A. | -4 | B. | -3 | C. | -2 | D. | -1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
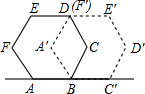 如图,将正六边形ABCDEF绕点B顺时针旋转后到达A′BC′D′E′F′的位置,所转过的度数是( )
如图,将正六边形ABCDEF绕点B顺时针旋转后到达A′BC′D′E′F′的位置,所转过的度数是( )| A. | 60° | B. | 72° | C. | 108° | D. | 120° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com