
”¾ĢāÄæ”æij¹¤³§¼Ę»®Éś²ś¼×”¢ŅŅĮ½ÖÖ¼¾½ŚŠŌ²śĘ·,ŌŚ“ŗ¼¾ÖŠ,¼×ÖÖ²śĘ·ŹŪ¼Ū50Ē§ŌŖ/¼ž,ŅŅÖÖ²śĘ·ŹŪ¼Ū30Ē§ŌŖ/¼ž,Éś²śÕāĮ½ÖÖ²śĘ·ŠčŅŖA”¢BĮ½ÖÖŌĮĻ.
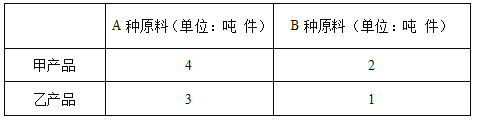
Ćæøö¼¾½ŚøĆ³§ÄÜ»ńµĆAÖÖŌĮĻ120¶Ö,BÖÖŌĮĻ50¶Ö
(1)ČēŗĪ°²ÅÅÉś²ś,²ÅÄÜĒ”ŗĆŹ¹Į½ÖÖŌĮĻČ«²æÓĆĶź,“ĖŹ±×ܲśÖµŹĒ¶ąÉŁĶņŌŖ.
(2)ŌŚĻļ¾ÖŠ¼×ÖÖ²śĘ·ŹŪ¼ŪÉĻÕĒ![]() ,¶ųŅŅÖÖ²śĘ·ŹŪ¼ŪĻĀ½µ
,¶ųŅŅÖÖ²śĘ·ŹŪ¼ŪĻĀ½µ![]() ,²¢ĒŅŅŖĒó¼×ÖÖ²śĘ·±ČŅŅÖÖ²śĘ·¶ąÉś²ś20¼ž,ĪŹČēŗĪ°²Åżה¢ŅŅĮ½ÖÖ²śĘ·µÄÉś²ś,Ź¹×ܲśÖµŹĒ1264Ē§ŌŖ.
,²¢ĒŅŅŖĒó¼×ÖÖ²śĘ·±ČŅŅÖÖ²śĘ·¶ąÉś²ś20¼ž,ĪŹČēŗĪ°²Åżה¢ŅŅĮ½ÖÖ²śĘ·µÄÉś²ś,Ź¹×ܲśÖµŹĒ1264Ē§ŌŖ.
”¾“š°ø”æ£Ø1£©Éś²ś¼×ÖÖ²śĘ·15¼ž,Éś²śŅŅÖÖ²śĘ·20¼ž²ÅÄÜĒ”ŗĆŹ¹Į½ÖÖŌĮĻČ«²æÓĆĶź,“ĖŹ±×ܲśÖµŹĒ135ĶņŌŖ£»£Ø2£©°²ÅÅÉś²ś¼×ÖÖ²śĘ·22¼ž,ŅŅÖÖ²śĘ·2¼žŹ¹×ܲśÖµŹĒ1264Ē§ŌŖ£®
”¾½āĪö”æ
£Ø1£©ÉčÉś²ś¼×ÖÖ²śĘ·x¼ž,Éś²śŅŅÖÖ²śĘ·y¼ž£¬øł¾ŻÉś²śøÕŗĆÓĆĶźĖłÓŠŌĮĻ£¬æÉĮŠ³ö·½³Ģ×éĒó³ö¼×ŅŅĮ½ÖÖ²śĘ·µÄ²śĮ棬ŌŁøł¾ŻŹŪ¼Ū¼ĘĖć×ܲśÖµ£»
£Ø2£©ÉčŅŅÖÖ²śĘ·Éś²śm¼ž, ŌņÉś²ś¼×ÖÖ²śĘ·(m+20)¼ž£¬·Ö±š¼ĘĖć³ö¼×ŅŅĮ½ÖÖ²śĘ·µÄ²śÖµ£¬øł¾Ż×ܲśÖµŹĒ1264Ē§ŌŖĮŠ³ö·½³ĢĒó½ā.
½ā£ŗ£Ø1£©ÉčÉś²ś¼×ÖÖ²śĘ·x¼ž,Éś²śŅŅÖÖ²śĘ·y¼ž,ŅĄĢāŅāÓŠ
![]() £¬½āµĆ
£¬½āµĆ![]() ,
,
![]() Ē§ŌŖ,
Ē§ŌŖ,
1350Ē§ŌŖ=135ĶņŌŖ£®
“š£ŗÉś²ś¼×ÖÖ²śĘ·15¼ž,Éś²śŅŅÖÖ²śĘ·20¼ž²ÅÄÜĒ”ŗĆŹ¹Į½ÖÖŌĮĻČ«²æÓĆĶź,“ĖŹ±×ܲśÖµŹĒ135ĶņŌŖ£»
£Ø2£©ÉčŅŅÖÖ²śĘ·Éś²śm¼ž,ŌņÉś²ś¼×ÖÖ²śĘ·(m+20)¼ž,ŅĄĢāŅāÓŠ
(1+10%)”Į50(m+20)+(1-10%)”Į20m=1264,
½āµĆm=2, m+20=22,
“ĖŹ±ĻūŗÄAŌĮĻ22”Į4+2”Į3=94£¼120£¬
ĻūŗÄBŌĮĻ22”Į2+2”Į1=46£¼50£¬
ĖłŅŌÕāŃł°²ÅÅæÉŠŠ£¬
“š£ŗ°²ÅÅÉś²ś¼×ÖÖ²śĘ·22¼ž,ŅŅÖÖ²śĘ·2¼žŹ¹×ܲśÖµŹĒ1264Ē§ŌŖ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖĒģ×£½Ø¹śĘߏ®ÖÜÄź£¬ÄĻøŚĒų×¼±ø¶ŌijµĄĀ·¹¤³Ģ½ųŠŠøÄŌģ£¬ČōĒė¼×¹¤³Ģ¶Óµ„¶Ą×ö“Ė¹¤³ĢŠč4øöŌĀĶź³É£¬ČōĒėŅŅ¹¤³Ģ¶Óµ„¶Ą×ö“Ė¹¤³ĢŠč6øöŌĀĶź³É£¬Čō¼×”¢ŅŅĮ½¶ÓŗĻ×÷2øöŌĀŗ󣬼׹¤³Ģ¶Óµ½ĘŚ³·Ąė£¬ŌņŅŅ¹¤³Ģ¶ÓŌŁµ„¶ĄŠč¼øøöŌĀÄÜĶź³É£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĘ½Ä³ÓĪÓ¾¹ŻŹīĘŚĶĘ³öĮ½ÖÖÓĪÓ¾ø¶·Ń·½Ź½£¬·½Ź½Ņ»£ŗĻČ¹ŗĀņ»įŌ±Ö¤£¬ĆæÕÅ»įŌ±Ö¤100ŌŖ£¬Ö»ĻŽ±¾ČĖµ±ÄźŹ¹ÓĆ£¬Ę¾Ö¤ÓĪÓ¾Ćæ“ĪŌŁø¶·Ń20ŌŖ£»·½Ź½¶ž£ŗ²»¹ŗĀņ»įŌ±Ö¤£¬Ćæ“ĪÓĪÓ¾ø¶·Ń25ŌŖ£®É芔Ć÷¼Ę»®½ńÄźŹīĘŚÓĪÓ¾“ĪŹżĪŖx£ØxĪŖÕżÕūŹż£©£®øł¾ŻĢāŅāĮŠ±ķ£ŗ
ÓĪÓ¾“ĪŹż | 5 | 8 | 10 | ” | x |
·½Ź½Ņ»µÄ×Ü·ŃÓĆ£Ø | 200 | 260 | m | ” | |
·½Ź½¶žµÄ×Ü·ŃÓĆ£Ø | 125 | 200 | 250 | ” |
£Ø1£©±ķøńÖŠµÄmÖµĪŖ £»
£Ø2£©øł¾ŻĢāŅā·Ö±šĒó³öĮ½ÖÖø¶·Ń·½Ź½ÖŠ![]() Óė×Ō±äĮæxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½²¢»³öĶ¼Ļó£»
Óė×Ō±äĮæxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½²¢»³öĶ¼Ļó£»
£Ø3£©ĒėÄćøł¾ŻĶ¼Ļ󣬰ļÖśŠ”Ć÷Éč¼ĘŅ»ÖÖ±Č½ĻŹ”Ē®µÄø¶·Ń·½°ø£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖŹżÖįÉĻµćA±ķŹ¾µÄŹżĪŖ©3£¬BŹĒŹżÖįÉĻĪ»ÓŚµćAÓŅ²ąŅ»µć£¬ĒŅAB£½12£®¶ÆµćP“ÓµćA³ö·¢£¬ŅŌĆæĆė2øöµ„Ī»³¤¶ČµÄĖŁ¶ČŃŲŹżÖįĻņµćB·½ĻņŌČĖŁŌĖ¶Æ£¬ÉčŌĖ¶ÆŹ±¼äĪŖtĆė£®
£Ø1£©ŹżÖįÉĻµćB±ķŹ¾µÄŹżĪŖ”” ””£»µćP±ķŹ¾µÄŹżĪŖ”” ””£ØÓĆŗ¬tµÄ“śŹżŹ½±ķŹ¾£©£®
£Ø2£©¶ÆµćQ“ÓµćB³ö·¢£¬ŅŌĆæĆė1øöµ„Ī»³¤¶ČµÄĖŁ¶ČŃŲŹżÖįĻņµćA·½ĻņŌČĖŁŌĖ¶Æ£»µćP”¢µćQĶ¬Ź±³ö·¢£¬µ±µćPÓėµćQÖŲŗĻŗ󣬵ćPĀķÉĻøı䷽Ļņ£¬ÓėµćQ¼ĢŠųĻņµćA·½ĻņŌČĖŁŌĖ¶Æ£ØµćP”¢µćQŌŚŌĖ¶Æ¹ż³ĢÖŠ£¬ĖŁ¶ČŹ¼ÖÕ±£³Ö²»±ä£©£»µ±µćP·µ»Ųµ½“ļAµćŹ±£¬P”¢QĶ£Ö¹ŌĖ¶Æ£®ÉčŌĖ¶ÆŹ±¼äĪŖtĆė£®
¢Łµ±µćP·µ»Ųµ½“ļAµćŹ±£¬ĒótµÄÖµ£¬²¢Ēó³ö“ĖŹ±µćQ±ķŹ¾µÄŹż£®
¢Śµ±µćPŹĒĻ߶ĪAQµÄČżµČ·ÖµćŹ±£¬ĒótµÄÖµ£®
![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬°ŃRt”÷ABC·ÅŌŚÖ±½Ē×ų±źĻµÄŚ£¬ĘäÖŠ”ĻCAB£½90”ć£¬BC£½5£¬µćA£¬BµÄ×ų±ź·Ö±šĪŖ(1£¬0)£¬(4£¬0)£¬½«”÷ABCŃŲxÖįĻņÓŅĘ½ŅĘ£¬µ±µćCĀäŌŚÖ±Ļßy£½2x£6ÉĻŹ±£¬Ļ߶ĪBCÉعżµÄĆ껿ĪŖ________£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
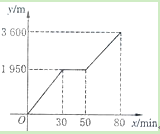
”¾ĢāÄæ”抔ӱŗĶŠ”ĮĮÉĻɽÓĪĶę£¬Š”Ó±³Ė×ųĄĀ³µ£¬Š”ĮĮ²½ŠŠ£¬Į½ČĖĻąŌ¼ŌŚÉ½¶„µÄĄĀ³µÖÕµć»įŗĻ£®ŅŃÖŖŠ”ĮĮŠŠ×ßµ½ĄĀ³µÖÕµćµÄĀ·³ĢŹĒĄĀ³µµ½É½¶„µÄĻßĀ·³¤µÄ2±¶£®Š”Ó±ŌŚŠ”ĮĮ³ö·¢ŗó50min ²Å³ĖÉĻĄĀ³µ£¬ĄĀ³µµÄĘ½¾łĖŁ¶ČĪŖ180m/min£®É芔ĮĮ³ö·¢x minŗóŠŠ×ßµÄĀ·³ĢĪŖy m£¬Ķ¼ÖŠ µÄÕŪĻß±ķŹ¾Š”ĮĮŌŚÕūøöŠŠ×ß¹ż³ĢÖŠyÓėxµÄŗÆŹż¹ŲĻµ£®
£Ø1£©Š”ĮĮŠŠ×ßµÄ×ÜĀ·³ĢŹĒ___________m£¬ĖūĶ¾ÖŠŠŻĻ¢ĮĖ_____________min£»
£Ø2£©¢Łµ±50£¼x£¼80Ź±£¬ĒóyÓėxµÄŗÆŹż¹ŲĻµŹ½£»¢Śµ±Š”Ó±µ½“ļĄĀ³µÖÕµćŹ±£¬Š”ĮĮĄėĄĀ³µÖÕµćµÄĀ·³ĢŹĒ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĖę×ųöŠŠ·½Ź½µÄ¶ąŃł»Æ£¬Ä³µŲĒų“ņ³µÓŠČżÖÖ³Ė³µ·½Ź½£¬ŹÕ·Ń±ź×¼ČēĻĀ£Ø¼ŁÉč“ņ³µµÄĘ½¾ł³µĖŁĪŖ30Ē§Ć×/Š”Ź±£©£ŗ
ĶųŌ¼³ö×ā³µ | ĶųŌ¼Ė³·ē³µ | ĶųŌ¼×سµ |
3Ē§Ć×ŅŌÄŚ£ŗ12ŌŖ | 1.5ŌŖ/Ē§Ć× | 2ŌŖ/Ē§Ć× |
³¬¹ż3Ē§Ć׵IJæ·Ö£ŗ2.4ŌŖ/Ē§Ć× | 0.5ŌŖ/·ÖÖÓ | 0.6ŌŖ/·ÖÖÓ |
£ØČē£ŗ³Ė×ų6Ē§Ć×£¬ŗÄŹ±12·ÖÖÓ£¬ĶųŌ¼³ö×ā³µµÄŹÕ·ŃĪŖ£ŗ12+2.4”Į£Ø6-3£©=19.2£ØŌŖ£©£»ĶųŌ¼Ė³·ē³µµÄŹÕ·ŃĪŖ£ŗ6”Į1.5+12”Į0.5=15£ØŌŖ£©£»ĶųŌ¼×سµµÄŹÕ·ŃĪŖ£ŗ6”Į2+12”Į0.6=19.2£ØŌŖ£©£©
Ēė¾Ż“ĖŠÅĻ¢½ā¾öČēĻĀĪŹĢā£ŗ
£Ø1£©ĶõĄĻŹ¦³Ė³µ“ÓׯčžŌ°Č„Ęū³µÕ¾£¬Č«³Ģ8Ē§Ć×£¬Čē¹ūĶõĄĻŹ¦³Ė×ųĶųŌ¼³ö×ā³µ£¬ŠčŅŖÖ§ø¶µÄ“ņ³µ·ŃÓĆĪŖ______ŌŖ£»
£Ø2£©ĄīŠ£³¤³Ė³µ“ÓׯµōŌ°Č„ÉśĢ¬Ō°£¬³Ė×ųĶųŌ¼Ė³·ē³µ±Č³Ė×ųĶųŌ¼³ö×ā³µ½ŚŹ”ĮĖ2ŌŖ£®Ēó“ÓׯčžŌ°Č„ÉśĢ¬Ō°µÄĀ·³Ģ£»
£Ø3£©ĶųŌ¼×سµĪŖĮĖŗĶĶųŌ¼Ė³·ē³µ¾ŗÕłæĶ»§£¬·Ö±šĶĘ³öĮĖÓÅ»Ż·½Ź½£ŗĶųŌ¼Ė³·ē³µ¶ŌÓŚ³Ė³µĀ·³ĢŌŚ5Ē§Ć×ŅŌÉĻ£Øŗ¬5Ē§Ć×£©µÄæĶ»§Ćæ“ĪŹÕ·ŃĮ¢¼õ6ŌŖ£»ĶųŌ¼×سµ“ņ³µ³µ·ŃŅ»ĀÉĘßĪåÕŪÓÅ»Ż£®¶Ō²ÉÓĆÄÄŅ»ÖÖ“ņ³µ·½Ź½øüŗĻĖćĢį³öÄćµÄ½ØŅ飮
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
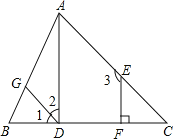
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ![]() £¬
£¬![]() £¬
£¬![]() ŹŌĖµĆ÷Ö±ĻßADÓėBC“¹Ö±
ŹŌĖµĆ÷Ö±ĻßADÓėBC“¹Ö±![]() ĒėŌŚĻĀĆęµÄ½ā“š¹ż³ĢµÄæÕøńÄŚĢīæÕ»ņŌŚĄØŗÅÄŚĢīŠ“ĄķÓÉ
ĒėŌŚĻĀĆęµÄ½ā“š¹ż³ĢµÄæÕøńÄŚĢīæÕ»ņŌŚĄØŗÅÄŚĢīŠ“ĄķÓÉ![]() £®
£®
ĄķÓÉ£ŗ![]() £¬
£¬![]() ŅŃÖŖ
ŅŃÖŖ![]()
![]() ______
______![]() ______£¬
______£¬![]() ______
______![]()
![]() ______
______![]() ______
______![]()
ÓÖ![]() £¬
£¬![]() ŅŃÖŖ
ŅŃÖŖ![]()
![]() ______
______![]() µČĮæ“ś»»
µČĮæ“ś»»![]()
![]() ______
______![]() ______£¬
______£¬![]() ______
______![]()
![]() ______
______![]()
![]() £¬
£¬![]() ŅŃÖŖ
ŅŃÖŖ![]()
![]() £¬
£¬![]() £¬
£¬
![]() ______
______![]() ______£®
______£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£Ø1£©ŅŃÖŖy©2Óėx³ÉÕż±ČĄż£¬ĒŅx£½2Ź±£¬y£½©6£®¢ŁĒóyÓėxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£»¢Śµ±y£¼3Ź±£¬ĒóxµÄȔֵ·¶Ī§£®
£Ø2£©ŅŃÖŖ¾¹żµć£Ø©2£¬©2£©µÄÖ±Ļßl1£ŗy1£½mx+nÓėÖ±Ļßl2£ŗy2£½©2x+6Ļą½»ÓŚµćM£Ø1£¬p£©
¢Ł¹ŲÓŚx£¬yµÄ¶žŌŖŅ»“Ī·½³Ģ×é![]() µÄ½āĪŖ”” ””£»¢ŚĒóÖ±Ļßl1µÄ±ķ“ļŹ½£®
µÄ½āĪŖ”” ””£»¢ŚĒóÖ±Ļßl1µÄ±ķ“ļŹ½£®
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com