
【题目】商店销售某上市新品,期间共销售该产品![]() 天,设销售时间为
天,设销售时间为![]() 天,第一天销售单价定为
天,第一天销售单价定为![]() 元/千克,售出
元/千克,售出![]() 千克.从第
千克.从第![]() 天至第
天至第![]() 天,该产品成本价为
天,该产品成本价为![]() 元/千克,销售单价每天降低
元/千克,销售单价每天降低![]() 元,销售量每天增加
元,销售量每天增加![]() 千克.从第
千克.从第![]() 天开始,成本价降为
天开始,成本价降为![]() 元/千克,销售单价稳定在
元/千克,销售单价稳定在![]() 元/千克,每天销售量
元/千克,每天销售量![]() (千克)与第
(千克)与第![]() 天满足一次函数关系
天满足一次函数关系![]() ,设第
,设第![]() 天销售利润为
天销售利润为![]() 元
元
![]() 直接写出
直接写出![]() 与
与![]() 的函数关系式;
的函数关系式;
![]() 问销售该商品第几天时,当天销售利润最大,最大利润是多少?
问销售该商品第几天时,当天销售利润最大,最大利润是多少?
![]() 该商品在这
该商品在这![]() 天的销售过程中,共有多少天每天销售利润不低于
天的销售过程中,共有多少天每天销售利润不低于![]() 元?
元?
【答案】(1)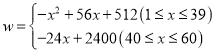 ;(2)销售该商品第
;(2)销售该商品第![]() 天时,当天销售利润最大,最大利润是
天时,当天销售利润最大,最大利润是![]() 元;(3)当有
元;(3)当有![]() 天,每天销售利润不低
天,每天销售利润不低![]() 元
元
【解析】
(1)需要分情况讨论,第一阶段时间在![]() ,第二阶段
,第二阶段![]() ,根据题意列式化简即可;
,根据题意列式化简即可;
(2)分别计算第一阶段,第二阶段的最大利润,两者相比较,最大的即作为最大利润;
(3)分别计算第一阶段,第二阶段利润不低于1232元的天数,两者相加即可.
解:(1)由题意可得,可列方程,
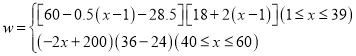
整理得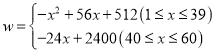
(2)由(1)得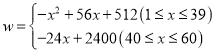
![]() 当
当![]() 时,
时,![]()
![]()
![]() 时,有最大值
时,有最大值
即当![]() 时,最大利润为
时,最大利润为![]() 元
元
当![]() 时,
时,![]()
![]()
![]() 随着
随着![]() 的增大而减少
的增大而减少
![]() 时有最大值
时有最大值
即![]()
综上所述,销售该商品第![]() 天时,当天销售利润最大,最大利润是
天时,当天销售利润最大,最大利润是![]() 元.
元.
![]() 当
当![]() 时,
时,![]()
得![]()
![]() 为整数
为整数
![]()
共计9天
![]() 当
当![]() 时,有
时,有![]()
解得![]()
![]() 时,
时,![]()
共计17天
∵![]()
故有![]() 天,每天销售利润不低
天,每天销售利润不低![]() 于元
于元


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c和直线y=x+1交于A,B两点,点A在x轴上,点B在直线x=3上,直线x=3与x轴交于点C
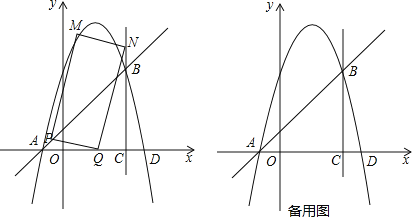
(1)求抛物线的解析式;
(2)点P从点A出发,以每秒![]() 个单位长度的速度沿线段AB向点B运动,点Q从点C出发,以每秒2个单位长度的速度沿线段CA向点A运动,点P,Q同时出发,当其中一点到达终点时,另一个点也随之停止运动,设运动时间为t秒(t>0).以PQ为边作矩形PQNM,使点N在直线x=3上.
个单位长度的速度沿线段AB向点B运动,点Q从点C出发,以每秒2个单位长度的速度沿线段CA向点A运动,点P,Q同时出发,当其中一点到达终点时,另一个点也随之停止运动,设运动时间为t秒(t>0).以PQ为边作矩形PQNM,使点N在直线x=3上.
①当t为何值时,矩形PQNM的面积最小?并求出最小面积;
②直接写出当t为何值时,恰好有矩形PQNM的顶点落在抛物线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的半圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB、FC.
(1)求证:四边形ABFC是菱形;
(2)若AD=![]() ,BE=1,求半圆的面积.
,BE=1,求半圆的面积.
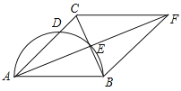
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组对函数![]() 的图象和性质进行了研究,探究过程如下.
的图象和性质进行了研究,探究过程如下.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下.
x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 8 | m | 0 | 2 | n | 2 | 0 |
| 8 | … |
其中,m= ,n= ;
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请补全函数图象的剩余部分;
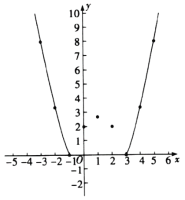
(3)进一步探究函数图象发现:
①函数图象与x轴有_____________个交点;
②方程![]() 有_____________个实数根;
有_____________个实数根;
③当关于x的方程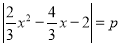 有3个实数根时,p的值是_____________.
有3个实数根时,p的值是_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解初中学生每天在校体育活动的时间(单位:![]() ),随机调查了该校的部.分学生,根据调查结果绘制出如下统计图:
),随机调查了该校的部.分学生,根据调查结果绘制出如下统计图:
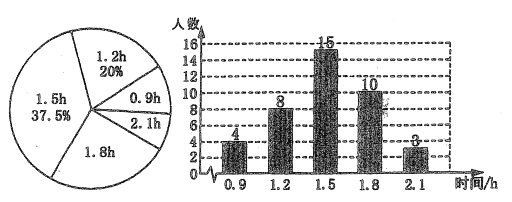
(1)求调查的学生是多少人? .
(2)求调查的学生每天在校体育活动时间的平均数、众数;
(3)若该校有![]() 名初中学生,估计该校每天在校体育活动时间大于
名初中学生,估计该校每天在校体育活动时间大于![]() 的学生人数.
的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
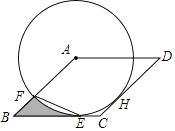
【题目】如图,已知⊙A与菱形ABCD的边BC相切于点E,与边AB相交于点F,连接EF.
(1)求证:CD是⊙A的切线;
(2)若⊙A的半径为2,tan∠BEF=![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
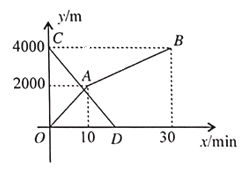
【题目】小玲和弟弟小东分别从家和图书馆同时出发,沿同一条路相向而行,小玲开始跑步中途改为步行,到达图书馆恰好用![]() .小东骑自行车以
.小东骑自行车以![]() 的速度直接回家,两人离家的路程
的速度直接回家,两人离家的路程![]() 与各自离开出发 地的时间之间
与各自离开出发 地的时间之间![]() 的函数图象如图所示.
的函数图象如图所示.
![]() 家与图书馆之间的路程为多少
家与图书馆之间的路程为多少![]() ,小玲步行的速度为多少
,小玲步行的速度为多少![]() ;
;
![]() 求小东离家的路程
求小东离家的路程![]() 关于
关于![]() 的函数解析式,并写出自变量的取值范围;
的函数解析式,并写出自变量的取值范围;
![]() 求两人相遇时离家多远?
求两人相遇时离家多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com