
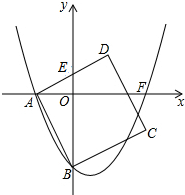
 ��ͼ�����κ���y=ax2+bx-4m��a��0����x�Ḻ���ύ�ڵ�A����y�Ḻ���ύ�ڵ�B��������ABCD�ı�AD��y�������ύ��E��0��m����
��ͼ�����κ���y=ax2+bx-4m��a��0����x�Ḻ���ύ�ڵ�A����y�Ḻ���ύ�ڵ�B��������ABCD�ı�AD��y�������ύ��E��0��m�������� ��1����õ�B������Ϊ��0��-4m����m��0��E��0��m�����ɵ�OE=m��OB=4m��֤����AOB����EOA���õ�OA2=OB•OE=4m2������OA=2m�����ɽ��
��2������C��y�ᴹ�ߣ�Ȼ���첢֤����AOB�ա�BGC����m��ʾ��C����F�����꣬����F��������������߽���ʽ�������ma��ֵ��
��3�����κ���y=x2+bx-4m��������ABCD�������ߣ������˵㣩ʼ�ն���������㣬���������������εĽ����ڵ�A�Ҳ࣬�ڵ�C����࣬��ǰ����õĵ�A��F���룬�õ���������ʽ�������������ʽ���ɵõ��𰸣�
��� �⣺��1���ߵ�x=0ʱ��y=ax2+bx-4m=-4m��
����κ���y=ax2+bx-4m��a��0��ͼ����Y�Ḻ���ύ�ڵ�B��0��-4m����m��0��
��������ABCD�ı�AD��y�������ύ��E��0��m����
��OE=m��
�ߡ�EAO+��AEO=90�㣬��EAO+��BOA=90�㣬
���AEO=��BOA��
�ߡ�AOE=��BOA��
���AOB����EOA��
��OA2=OB•OE=4m2
��OA=2m��
���A��������-2m��0����
��2������C��CG��y���ڵ�G����ͼ1��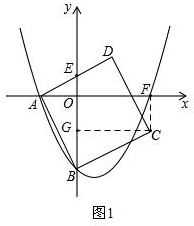
��ABO+��COB=90�㣬��COB+��BCG=90��
�ڡ�AOB�͡�BGC�У�
$\left\{\begin{array}{l}{��ABO=��BCG}\\{��AOB=��CGB}\\{AB=CB}\end{array}\right.$��
���AOB�ա�BGC��AAS����
��BG=AO��CG=BO��
��C��4m��-2m����
��CF��x�ᣬ
��F��4m��0����
��a��4m��2+b��4m��-4m=0��
4am=1-b��
8am=2-2b����
a��2m��2+b��-2m��-4m=0��
4am=4+2b����
��+�ڵõ�12am=6��
ma=$\frac{1}{2}$��
��3���߶��κ���y=x2+bx-4m��������ABCD�������ߣ������˵㣩ʼ�ն���������㣬����ͼ��
���������������εĽ����ڵ�A�Ҳ࣬�ڵ�C����࣬
��A��-2m��0����C��4m��-2m����
�൱x=-2m��y��0����x=4m��y��-2m��
������-2m��2+b����-2m��-4m��0�٣�
��4m��2+4bm-4m��-2m�ڣ�
��ٵã�4m2-2bm-4m��0��
��m��0��
��4m-2b-4��0�ۣ�
��ڵã�16m2+4bm-2m��0��
��m��0��
��8m+2b-1��0�ܣ�
��+�ܵã�
12m-5��0��
��m��$\frac{5}{12}$��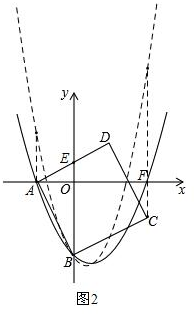
���� �����Ƕ��κ������ۺ����ͣ������漰����֪ʶ���У����κ����Ļ������ʡ������εĻ������ʡ�ȫ�������ε��ж������ʣ��ۺ�����ǿ���ѵ��������е�����궼������ĸ����ѧ�������⡢����������ߵ�Ҫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
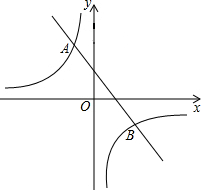 ��ͼ��һ�κ�����ͼ���뷴��������y=$\frac{{k}_{2}}{x}$��k2��0����ͼ����A��-2��6���͵�B��4��n��
��ͼ��һ�κ�����ͼ���뷴��������y=$\frac{{k}_{2}}{x}$��k2��0����ͼ����A��-2��6���͵�B��4��n���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
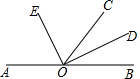 ��ͼ��O��ֱ��AB��һ�㣬OCΪ��һ�����ߣ�ODƽ�֡�BOC��OEƽ�֡�AOC
��ͼ��O��ֱ��AB��һ�㣬OCΪ��һ�����ߣ�ODƽ�֡�BOC��OEƽ�֡�AOC�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
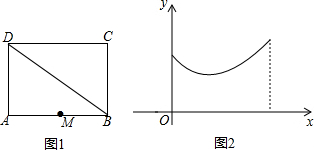 ��ͼ1��������ABCD�У���M��AB���е㣬��P��ij���߶��������˶������˶���ʱ��Ϊx����P���M֮��ľ���Ϊy���ұ�ʾy��x�ĺ�����ϵ��ͼ�������ͼ2��ʾ�����P���˶�·�߿����ǣ�������
��ͼ1��������ABCD�У���M��AB���е㣬��P��ij���߶��������˶������˶���ʱ��Ϊx����P���M֮��ľ���Ϊy���ұ�ʾy��x�ĺ�����ϵ��ͼ�������ͼ2��ʾ�����P���˶�·�߿����ǣ�������| A�� | A��B | B�� | A��D | C�� | B��D | D�� | D��C |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com