
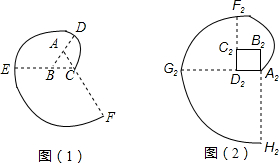
���� ��1������CDEF�ij��ɻ�CD����DE����EF��ɣ��������Ե�Բ�ĽǶ�Ϊ120�㣬���뾶�ֱ�Ϊ1��2��3�����ݻ�����ʽ�ֱ�������������������ǵĺͼ��ɣ�
��2����ȣ�1���ķ���������A2E2F2C2H2�ij���4������ɣ��������Ե�Բ�ĽǶ�Ϊ270�㣬���뾶�ֱ�Ϊ1��2��3��4�����ݻ�����ʽ�ֱ���㣬�ĸ������������ǵĺͼ��ɣ�
��3����һ���߳�Ϊ1��������ΰ����������������ߣ�����һ�ܺ����ߵij�������5������ɣ��������Ե�Բ�ĽǶ�Ϊ180��-$\frac{��5-2����180}{5}$=72�㣬���뾶�ֱ�Ϊ1��2��3��4��5�����ݻ�����ʽ�ֱ���㣬�ĸ������������ǵĺͼ��ɣ�
��4���ɼ���ó����ɣ�������⼴�ɣ�
��� �⣺��1���ߡ�ABC���������Σ�
���CAD=��DBE=��ECF=120�㣬
�֡�AB=1��
��AC=1��BD=2��CE=3��
��CD���ij���=$\frac{120��1}{180}$=$\frac{2}{3}$��
DE���ij���=$\frac{120��2}{180}$=$\frac{4}{3}$��
EF���ij���=$\frac{120��3}{180}$=2��
��������CDEF�ij�Ϊ$\frac{2}{3}$��+$\frac{4}{3}$��+2��=4�У�
��2����A2B2C2D2Ϊ�����Σ��߳�Ϊ1����һ�ܵ�����A2E2F2C2H2�ij�Ϊ$\frac{90�С�1}{180}$+$\frac{90�С�2}{180}$+$\frac{90�С�3}{180}$+$\frac{90�С�4}{180}$=5�У�
��3������һ���߳�Ϊ1��������ΰ����������������ߣ�����һ�ܺ����ߵij�����$\frac{72�С�1}{180}$+$\frac{72�С�2}{180}$+$\frac{72�С�3}{180}$+$\frac{72�С�4}{180}$+$\frac{72�С�5}{180}$=6�У�
��4����һ���߳�Ϊ1����n�������������������������ߣ���һ�ܺ�����߳��ǣ�n+1���У�
���� ������Ҫ������Բ���ۺ��⼰�����ļ��㣬����Ĺؼ�������n���ε������n�Ĺ�ϵ��Ȼ�������ý������е�n�صĹ�ϵ��ֵ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
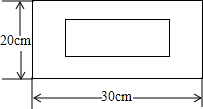 ��ͼ��ʾ����һ�鳤�������أ���Ϊ30m����Ϊ20m������������а�ͼ����ʾ�ķ�ʽ��һ����Ϊa m��С·�����µ�Ϊ�˵أ�
��ͼ��ʾ����һ�鳤�������أ���Ϊ30m����Ϊ20m������������а�ͼ����ʾ�ķ�ʽ��һ����Ϊa m��С·�����µ�Ϊ�˵أ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���̵Ľ���x=m | B�� | m��0ʱ�����̵Ľ������� | ||
| C�� | m��0ʱ�����̵Ľ������� | D�� | ����mȡ��ֵ�����̶������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
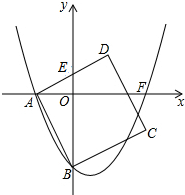 ��ͼ�����κ���y=ax2+bx-4m��a��0����x�Ḻ���ύ�ڵ�A����y�Ḻ���ύ�ڵ�B��������ABCD�ı�AD��y�������ύ��E��0��m����
��ͼ�����κ���y=ax2+bx-4m��a��0����x�Ḻ���ύ�ڵ�A����y�Ḻ���ύ�ڵ�B��������ABCD�ı�AD��y�������ύ��E��0��m�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
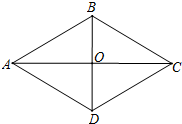 ��ͼ��������ABCD�У��Խ���AC��BD�ཻ�ڵ�O����BAD=60�㣬BD=4�������εı߳�AB�ͶԽ���AC�ij���
��ͼ��������ABCD�У��Խ���AC��BD�ཻ�ڵ�O����BAD=60�㣬BD=4�������εı߳�AB�ͶԽ���AC�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 С�������г��Ӽص��ҵأ���ͼ�����߱�ʾС��;������ʱ��t��h�����г�s��km��֮��ĺ�����ϵ��
С�������г��Ӽص��ҵأ���ͼ�����߱�ʾС��;������ʱ��t��h�����г�s��km��֮��ĺ�����ϵ���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com