
分析 根据不全相等的非零实数a,b,c满足$\frac{bc}{2{a}^{2}+bc}$+$\frac{ac}{2{b}^{2}+ac}$+$\frac{ab}{2{c}^{2}+ab}$=1,灵活变化,进行化简,分解因式,即可求得问题的答案.
解答 解:∵$\frac{bc}{2{a}^{2}+bc}$+$\frac{ac}{2{b}^{2}+ac}$+$\frac{ab}{2{c}^{2}+ab}$=1,
∴$\frac{bc}{2{a}^{2}+bc}+\frac{ac}{2{b}^{2}+ac}=1-\frac{ab}{2{c}^{2}+ab}$,
$\frac{b}{2{a}^{2}+bc}+\frac{a}{2{b}^{2}+ac}=\frac{2c}{2{c}^{2}+ab}$,
$\frac{{b}^{3}+abc+{a}^{3}}{(2{a}^{2}+bc)(2{b}^{2}+ac)}=\frac{c}{2{c}^{2}+ab}$,
c•(2a2+bc)(2b2+ac)=(2c2+ab)(b3+abc+a3),
化简,得
a3+b3+c3-3abc=0,
即(a+b+c)(a2+b2+c2-ab-ac-bc)=0,
∵a,b,c是不全相等的非零实数,
∴a2+b2+c2-ab-ac-bc≠0,
∴a+b+c=0.
即a+b+c的值是0.
点评 本题考查分式的化简求值,解题的关键是化简后再因式分解,然后根据题目中的信息进行讨论.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
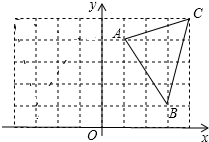 如图,平面直角坐标系,已知A(1,4),B(3,1),C(4,5).△ABC关于y轴的对称图形为△A1B1C1
如图,平面直角坐标系,已知A(1,4),B(3,1),C(4,5).△ABC关于y轴的对称图形为△A1B1C1查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
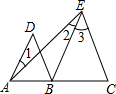 根据下列证明过程填空:
根据下列证明过程填空:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
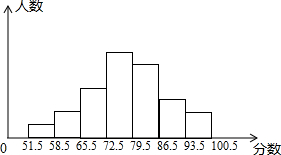 在一次中考模拟侧试中,某班的两名向学根据班级的成绩(分数为整数)分别绘制了频率分布统计表和频数分布直方图.在平频数分布直方图中从左到右每个小组的人数之比为1:2:4:7:6:3:2,其中93.5-100.5小组的人数为4人,请结合统计图表吗,回答下列问题:
在一次中考模拟侧试中,某班的两名向学根据班级的成绩(分数为整数)分别绘制了频率分布统计表和频数分布直方图.在平频数分布直方图中从左到右每个小组的人数之比为1:2:4:7:6:3:2,其中93.5-100.5小组的人数为4人,请结合统计图表吗,回答下列问题:| 分组 | 频率 |
| 52.5-60.5 | 0.06 |
| 60.5-68.5 | 0.08 |
| 68.5-76.5 | 0.24 |
| 76.5-84.5 | 0.30 |
| 84.5-92.5 | 0.20 |
| 92.5-100.5 | 0.12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
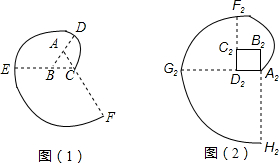
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com