
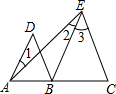
 根据下列证明过程填空:
根据下列证明过程填空: 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:选择题
| A. | 在图形上的每一点到旋转中心的距离相等 | |
| B. | 图形上每一点移动的角度相同 | |
| C. | 图形上任意两点的连线与其对应两点的连线长度相等 | |
| D. | 图形上可能存在不动的点 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
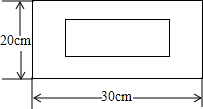 如图所示,有一块长方形土地,长为30m,宽为20m,在这块土地中按图中所示的方式修一条宽为a m的小路,余下的为菜地.
如图所示,有一块长方形土地,长为30m,宽为20m,在这块土地中按图中所示的方式修一条宽为a m的小路,余下的为菜地.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com