一个多边形的每个外角都是36°.则这个多边形是10边形.一个多边形的每一个内角都是135°.则这个多边形是8边形．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

4．一个多边形的每个外角都是36°，则这个多边形是10边形，一个多边形的每一个内角都是135°，则这个多边形是8边形．

分析（1）根据多边形的外角和是固定的360°，依此可以求出多边形的边数；
（2）已知每一个内角都等于135°，就可以知道每个外角是45度，根据多边形的外角和是360度就可以求出多边形的边数．

解答解：（1）∵一个多边形的每个外角都等于36°，
∴多边形的边数为360°÷36°=10，
故答案为：10；

（2）多边形的边数是：n=360°÷（180°-135°）=8．
故这个多边形是八边形．
故答案为：8．

点评本题考查了多边形内角与外角，通过本题要理解已知内角或外角求边数的方法．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：填空题

14．

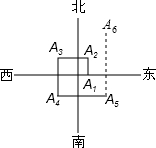如图，一个机器人从点O出发，向正东方向走3m到达点A₁，再向正北方向走6m到达点A₂，再向正西方向走9m到达点A₃，再向正南方向走12m到达点A₄，再向正东方向走15m到达点A₅．按如此规律下去，当机器人走到点A₆时，离点O的距离是15m．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

15．解方程：
（1）（x+2）²=4
（2）x²-5x-6=0．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

12．观察方程x+$\frac{1}{x}$=$\frac{5}{2}$，易知两根为x₁=2，x₂=$\frac{1}{2}$，x+$\frac{1}{x}$=$\frac{17}{4}$，两根x₁=4，x₂=$\frac{1}{4}$．根据其规律，则方程x+$\frac{1}{x-1}$=$\frac{13}{3}$两根为4或$\frac{4}{3}$．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

19．

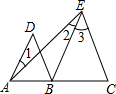根据下列证明过程填空：
∵∠1=∠2
∴AD∥BE（内错角相等，两直线平行）
∴∠D=∠DBE（两直线平行，内错角相等）
又∵∠D=∠3（已知）
∴∠DBE=∠3
∴BD∥CE（内错角相等，两直线平行）

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

9．已知直线y=2x-4+n经过原点，与反比例函数y=$\frac{n}{x}$的图象交于点A、B．求：
（1）反比例函数解析式；
（2）线段AB的长．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

16．

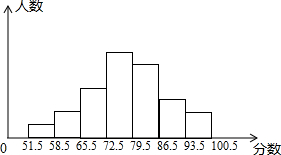在一次中考模拟侧试中，某班的两名向学根据班级的成绩（分数为整数）分别绘制了频率分布统计表和频数分布直方图．在平频数分布直方图中从左到右每个小组的人数之比为1：2：4：7：6：3：2，其中93.5-100.5小组的人数为4人，请结合统计图表吗，回答下列问题：

分组	频率
52.5-60.5	0.06
60.5-68.5	0.08
68.5-76.5	0.24
76.5-84.5	0.30
84.5-92.5	0.20
92.5-100.5	0.12

（1）求这个班级参加测试的人数；
（2）若这次测试成绩80分以上（含80分）为优秀，求优秀率；
（3）若这次测试成绩60分以上（含60分）为及格，则及格率可能是多少？

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

13．

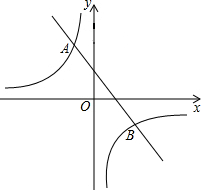如图，一次函数的图象与反比例函数y=$\frac{{k}_{2}}{x}$（k₂≠0）的图象交于A（-2，6）和点B（4，n）
（1）求反比例函数的解析式和直线AB的解析式；
（2）根据图象回答，在什么范围时，一次函数的值大于反比例函数的值；
（3）莲接0A，0B，求△AOB的面积．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

15．

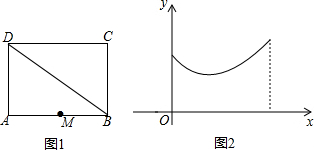如图1，正方形ABCD中，点M是AB的中点，点P在某条线段上匀速运动，若运动的时间为x，点P与点M之间的距离为y，且表示y与x的函数关系的图象大致如图2所示，则点P的运动路线可能是（　　）

A．

A→B

B．

A→D

C．

B→D

D．

D→C

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学