Question

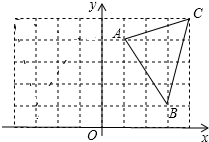
2．如图，平面直角坐标系，已知A（1，4），B（3，1），C（4，5）．△ABC关于y轴的对称图形为△A₁B₁C₁
（1）请画出△ABC关于y轴对称的△A₁B₁C₁；
（2）在坐标轴上取点D，使得△ABD为等腰三角形，这样的点D共有8个；
（3）若点P从点A处出发，向左平移m个单位．当点P落在△A₁B₁C₁（包括边）时，求m的取值范围．

Answer 1

分析 （1）首先确定A、B、C三点的对称点位置，再连接即可；
（2）根据等腰三角形的判定，分情况讨论：以A为圆心AB为半径画弧与y轴有2个交点，以B为圆心AB长为半径画弧与x轴有2个交点，与y轴2交点，作AB的垂直平分线与y轴有1个交点，与x轴1个交点；
（3）首先确定B₁C₁的直线解析式，然后再利用解析式确定N点坐标，进而可得m的取值范围．

解答 解：（1）如图所示：

（2）以A为圆心AB为半径画弧与y轴有2个交点，以B为圆心AB长为半径画弧与x轴有2个交点，与y轴2交点，作AB的垂直平分线与y轴有1个交点与x轴1个交点，因此这样的点D共有2+2+2+1+1=8个，
故答案为：8；

（3）设B₁C₁的直线解析式为y=kx+b，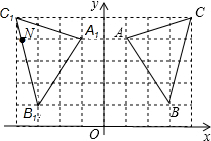
∵C₁（-4，5），B₁（-3，1），
∴$\left\{\begin{array}{l}{5=-4k+b}\\{1=-3k+b}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=-4}\\{b=-11}\end{array}\right.$，
∴B₁C₁的直线解析式为y=-4x-11，
当y=4时，x=-$\frac{15}{4}$，
∴N（-$\frac{15}{4}$，4），
∵点P从点A处出发，向左平移m个单位，
∴2≤m≤$\frac{19}{4}$．

点评 此题主要考查了作图--轴对称变换，以及等腰三角形的判定，在画一个图形的轴对称图形时，也是先从确定一些特殊的对称点开始的，一般的方法是：
①由已知点出发向所给直线作垂线，并确定垂足；
②直线的另一侧，以垂足为一端点，作一条线段使之等于已知点和垂足之间的线段的长，得到线段的另一端点，即为对称点；
③连接这些对称点，就得到原图形的轴对称图形．