
【题目】已知有公共顶点![]() 的△
的△![]() 和△
和△![]() 都是等边三角形,且
都是等边三角形,且![]() >
>![]() .
.

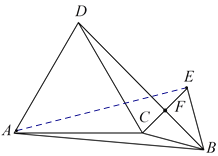
(1)如图1,当点![]() 恰好在
恰好在![]() 的延长线上时,连结
的延长线上时,连结![]() ,
,![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() .
.
①求证:![]() ;
;
②连接![]() ,求证:
,求证:![]() ∥
∥![]() ;
;
(2)图2是由图1中的△![]() 绕点
绕点![]() 顺时针旋转角
顺时针旋转角![]() (
(![]() <
<![]() <
<![]() )得到,使得
)得到,使得![]() 恰好经过
恰好经过![]() 的中点
的中点![]() ,试猜想线段
,试猜想线段![]() ,
,![]() ,
,![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
【答案】(1)①证明见解析;②证明见解析;(2)猜想:BC2+BD2=AB2,理由见解析.
【解析】
(1)①先由等边三角形得出CA=CD,CB=CE,∠ACD=∠BCE =60°,从而判断出∠ACE=∠DCB,得到△ACE≌△DCB,根据全等三角形的对应边相等即可得证;
②由∠ACD=∠BCE =60°可得∠MCN =60°,由△ACE≌△DCB可得∠CAE=∠CDB,然后根据ASA证明△ACM≌△DCN,从而得CM=CN,继而得到△MCN是等边三角形,进而根据平行线的判定即可得证;
(2)猜想:BC2+BD2=AB2,理由为:如图,连接AE,仿照(1)①证明△ACE≌△DCB,从而可得 AE=BD,∠AEC=∠DBC,再根据等边三角形的性质可得∠CBF=30°,继而可得∠AEB=∠AEC+∠BEC=90°,利用勾股定理可得AE2+BE2=AB2,等量代换即可得BC2+BD2=AB2.
(1)①∵△ACD,△BCE都是等边三角形,
∴∠DCA=∠BCE=60°,CA=CD,CB=CE,
∵∠ACE=∠ACD+∠MCN,∠DCB=∠MCN+∠BCE,
∴∠ACE=∠DCB,
∴△ACE≌△DCB(SAS),
∴AE=BD;
②∵A、C、B共线,∠ACD=∠BCE =60°,
∴∠MCN=180°-∠ACD-∠BCE=60°,
∴∠ACM=∠DCN,
∵△ACE≌△DCB,
∴∠CAM=∠CDN,
又∵CA=CD,
∴△ACM≌△DCN,
∴CM=CN,
又∵∠MCN=60°,
∴△MCN是等边三角形,
∴∠MNC=60°,
又∵∠BCE=60°,
∴∠MNC=∠BCE,
∴MN//AB;
(2)猜想:BC2+BD2=AB2,理由如下:
如图,连接AE,
∵△ACD,△BCE都是等边三角形,
∴∠DCA=∠BCE=∠BEC=∠CBE=60°,CA=CD,CB=CE=BE,
∵∠ACE=∠ACD+∠MCN,∠DCB=∠MCN+∠BCE,
∴∠ACE=∠DCB,
∴△ACE≌△DCB(SAS),
∴AE=BD,∠AEC=∠DBC,
又∵F为BC中点,
∴∠CBF=![]() ∠CBE=30°,
∠CBE=30°,
∴∠AEC=30°,
∴∠AEB=∠AEC+∠BEC=90°,
∴AE2+BE2=AB2,
∴BC2+BD2=AB2.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】某工程队承接了60万平方米的绿化工程,由于情况有变,……设原计划每天绿化的面积为![]() 万平方米,列方程为
万平方米,列方程为![]() ,根据方程可知省略的部分是( )
,根据方程可知省略的部分是( )
A. 实际工作时每天的工作效率比原计划提高了![]() 结果提前30天完成了这一任务
结果提前30天完成了这一任务
B. 实际工作时每天的工作效率比原计划提高了![]() ,结果延误30天完成了这一任务
,结果延误30天完成了这一任务
C. 实际工作时每天的工作效率比原计划降低了![]() ,结果延误30天完成了这一任务
,结果延误30天完成了这一任务
D. 实际工作时每天的工作效率比原计划降低了![]() ,结果提前30天完成了这一任务
,结果提前30天完成了这一任务
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC,垂足为D,AD=4,BD=2,CD=8.

(1)求证:∠BAC=90°;
(2)P为BC边上一点,连接AP,若△ABP为等腰三角形,请求出BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
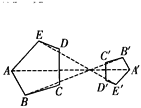
【题目】如图,五边形ABCDE与五边形A'B'C'D'E'是位似图形,且位似比为2.如果五边形ABCDE的面积为16 cm2,周长为20 cm,那么五边形A'B'C'D'E'的面积为_______,周长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小李骑自行车离家的距离![]() 与时间
与时间![]() 之间的关系.
之间的关系.
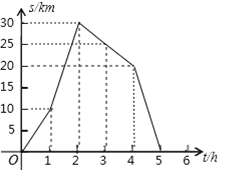
(1)在这个变化过程中自变量是______,因变量是______;
(2)小李何时到达离家最远的地方?此时离家多远?
(3)请直接写出小李何时与家相距![]() ?
?
(4)求出小李这次出行的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x1、x2是关于x的﹣元二次方程(a﹣6)x2+2ax+a=0的两个实数根.
(1)求a的取值范围;
(2)若(x1+1)(x2+1)是负整数,求实数a的整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某经销商准备进一批特色商品,经调查,用16000元采购A型商品的件数是用7500元采购B型商品的件数的2倍.一件A型商品的进价比一件B型商品的进价多10元.
(1)求一件A,B型商品的进价分别是多少?
(2)若经销商购进A,B型商品共250件,试销A型商品售价为240元/件,B型商品售价为220元/件,且全部售出.已知购进B型商品m件,A型商品的件数不小于B型商品的件数,且B型商品的销量不小于80件,试求销售完这批商品的最大利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,可以自由转动的转盘被3等分,指针落在每个扇形内的机会均等.
(1)现随机转动转盘一次,停止后,指针指向1的概率为 ;
(2)小明和小华利用这个转盘做游戏,若采用下列游戏规则,你认为对双方公平吗?请用列表或画树状图的方法说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com