【题目】如图，已知△ABC三个内角的平分线交于点O，点D在CA的延长线上，且DC=BC，AD=AO，若∠BAC=80°，则∠BCA的度数为 ．
【答案】60°.
【解析】
试题可证明△COD≌△COB，得出∠D=∠CBO，再根据∠BAC=80°，得∠BAD=100°，由角平分线可得∠BAO=40°，从而得出∠DAO=140°，根据AD=AO，可得出∠D=20°，即可得出∠CBO=20°，则∠ABC=40°，最后算出∠BCA=60°
试题解析：∵△ABC三个内角的平分线交于点O，
∴∠ACO=∠BCO，
在△COD和△COB中，
，
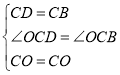∴△COD≌△COB，
∴∠D=∠CBO，
∵∠BAC=80°，
∴∠BAD=100°，
∴∠BAO=40°，
∴∠DAO=140°，
∵AD=AO，∴∠D=20°，
∴∠CBO=20°，
∴∠ABC=40°，
∴∠BCA=60°.
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
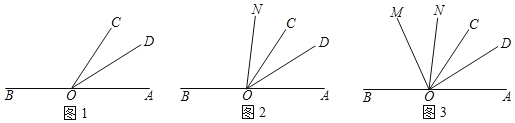
【题目】已知：点O为直线AB上一点，过点O作射线OC，使∠AOC=70°．
（1）如图1，若OD平分∠AOC，求∠DOB的度数；
（2）射线OM从OA出发，绕点O以每秒6°的速度逆时针旋转，同时，射线ON从OC出发绕点O以每秒4°的速度逆时针旋转，OM与ON同时出发(当ON首次与OB重合时，两条射线都停止运动)，设运动的时间为t秒．
(i)如图2，在整个运动过程中，当∠BON=2∠COM时，求t的值；
(ⅱ)如图3，OP平分∠AOM，OQ平分∠BON，是否存在合适的t，使OC平分∠POQ，若存在，求出t的值，若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
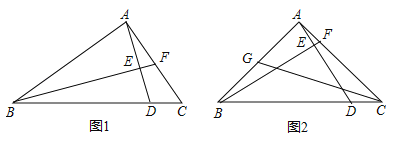
【题目】如图，直角△ABC中，∠BAC=90°，D在BC上，连接AD，作BF⊥AD分别交AD于E，AC于F．
（1）如图1，若BD=BA，求证：△ABE≌△DBE；
（2）如图2，若BD=4DC，取AB的中点G，连接CG交AD于M，求证：①GM=2MC；②AG2=AFAC．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，用棋子摆成的“上”字：
第一个“上”字 第二个“上”字 第三个“上”字
如果按照以上规律继续摆下去，那么通过观察，可以发现：
（1）第四、第五个“上”字分别需用 和 枚棋子．
（2）第n个“上”字需用 枚棋子．
（3）如果某一图形共有102枚棋子，你知道它是第几个“上”字吗？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，DE⊥AB于E，DF⊥AC于F,若BD=CD、BE=CF，
(1)求证：AD平分∠BAC；(2)已知AC=20， BE=4，求AB的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列图形都是由同样大小的圆按一定的规律组成，其中，第①个图形中一共有2个圆：第②个图形中一共有7个圆：第③个图形中一共有16个圆；第④个图形中一共有29个圆，…，则第⑦个图形中圆的个数为_______．
查看答案和解析>>
科目：初中数学 来源： 题型：
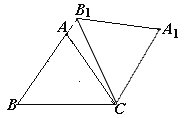
【题目】在△ABC中，AB＝AC＝5，cos∠ABC＝
，将△ABC绕点C顺时针旋转，得到△A1B1C．
（1）如图①，当点B1在线段BA延长线上时．①求证：BB1∥CA1；②求△AB1C的面积；
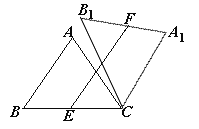
（2）如图②，点E是BC边的中点，点F为线段AB上的动点，在△ABC绕点C顺时针旋转过程中，点F的对应点是F1，求线段EF1长度的最大值与最小值的差．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知在纸面上有一数轴（如图），折叠纸面．
（1）若1表示的点与
表示的点重合，则
表示的点与数 表示的点重合；
（2）若表示的点与3表示的点重合，回答以下问题：
①5表示的点与数 表示的点重合；
②若数轴上
、
两点之间的距离为9（在的左侧），且、两点经折叠后重合，求、两点表示的数是多少？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
