
【题目】在△ABC中,AB=AC=5,cos∠ABC=![]() ,将△ABC绕点C顺时针旋转,得到△A1B1C.
,将△ABC绕点C顺时针旋转,得到△A1B1C.
(1)如图①,当点B1在线段BA延长线上时.①求证:BB1∥CA1;②求△AB1C的面积;
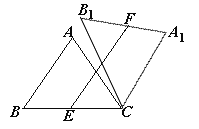
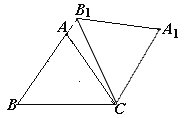
(2)如图②,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1,求线段EF1长度的最大值与最小值的差.
【答案】(1)①证明见试题解析;②![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)①根据旋转的性质和平行线的性质证明;
②过A作AF⊥BC于F,过C作CE⊥AB于E,根据等腰三角形的性质和三角形的面积公式解答;
(2)过C作CF⊥AB于F,以C为圆心CF为半径画圆交BC于F1,和以C为圆心BC为半径画圆交BC的延长线于F1,得出最大和最小值解答即可.
试题解析:(1)①证明:∵AB=AC,B1C=BC,
∴∠AB1C=∠B,∠B=∠ACB,
∵∠AB1C=∠ACB(旋转角相等),
∴∠B1CA1=∠AB1C,
∴BB1∥CA1;
②过A作AF⊥BC于F,过C作CE⊥AB于E,如图1:
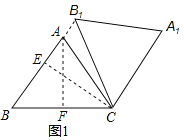
∵AB=AC,AF⊥BC,BC=6,
∴BF=CF=3,
∴B1C=BC=6,
可得:B1B=2BE,
∵EC=![]() ,
,
∴BE=![]() ,则BB1=
,则BB1=![]() ,
,
故AB1=![]() ﹣5=
﹣5=![]() ,
,
∴△AB1C的面积为:![]() ;
;
(2)如图2,过C作CF⊥AB于F,以C为圆心CF为半径画圆交BC于F1,EF1有最小值,
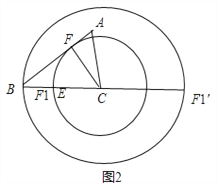
此时在Rt△BFC中,CF=![]() ,
,
∴CF1=![]() ,
,
∴EF1的最小值为![]() ﹣3=
﹣3=![]() ;
;
如图,以C为圆心BC为半径画圆交BC的延长线于F1,EF1有最大值;
此时EF1=EC+CF1=3+6=9,
∴线段EF1的最大值与最小值的差为9﹣![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=32cm,DE是AB的垂直平分线,分别交AB、AC于D、E两点.(1)若∠C=70°,则∠BEC=______度;(2)若BC=21cm,则△BCE的周长是______cm.
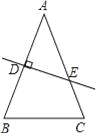
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小傅某天下午营运全是在东西走向的大道上行驶的.若如果规定向东为正,则行车里程(单位:km)如下:
+11,-2,+3,+10,-11,+5,-15,-8
(1)当把最后一名乘客送到目的地时,小傅距离出车地点的距离为多少?
(2)若每千米的营运额为7元,成本为1.5元/km,则这天下午他盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠ABC=∠BCD=90°,点E在BC边上,∠AED=90°
(1)求证:∠BAE=∠CED;(2)若AB+CD=DE,求证:AE+BE=CE
(3)在(2)的条件下,若△CDE与△ABE的面积的差为18,CD=6,求BE的长.
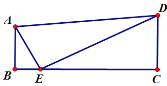


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司就上宽带网推出A,B,C三种月收费方式.这三种收费方式每月所需的费用y(元![]() 与上网时间x(h)的函数关系如图所示,则下列判断错误的是
与上网时间x(h)的函数关系如图所示,则下列判断错误的是![]()
![]()
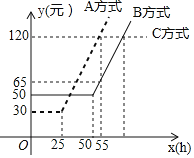
A. 每月上网时间不足25h时,选择A方式最省钱 B. 每月上网费用为60元时,B方式可上网的时间比A方式多
C. 每月上网时间为35h时,选择B方式最省钱 D. 每月上网时间超过70h时,选择C方式最省钱
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】窗户的形状如图所示(图中长度单位:cm),其中上部是半圆形,下部是边长相同的四个小正方形. 已知下部小正方形的边长是acm.
(1)计算窗户的面积(计算结果保留π).
(2)计算窗户的外框的总长(计算结果保留π).
(3)安装一种普通合金材料的窗户单价是175元/平方米,当a=50cm时,请你帮助计算这个窗户安装这种材料的费用(π≈3.14,窗户面积精确到0.1).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 分别为数轴上的两点,
分别为数轴上的两点,![]() 点对应的数为-20,
点对应的数为-20,![]() 点对应的数为100.
点对应的数为100.

(1)请写出![]()
![]() 中点
中点![]() 所对应的数;
所对应的数;
(2)现有一只电子蚂蚊![]() 从
从![]() 点出发,以6单位秒的速度向左运动,同时另一只电子蚂蚁
点出发,以6单位秒的速度向左运动,同时另一只电子蚂蚁![]() 恰好从
恰好从![]() 点出发,以4单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的
点出发,以4单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的![]() 点相遇,求
点相遇,求![]() 点对应的数.
点对应的数.
(3)若当电子蚂蚁![]() 从
从![]() 点出发时,以6单位/秒的速度向左运动,同时另一只电子蚂蚁
点出发时,以6单位/秒的速度向左运动,同时另一只电子蚂蚁![]() 恰好从
恰好从![]() 点出发,以4单位/秒的速度也向左运动,设两只电子蚂蚁在数轴上的
点出发,以4单位/秒的速度也向左运动,设两只电子蚂蚁在数轴上的![]() 点相遇,求
点相遇,求![]() 点对应的数.
点对应的数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com