
【题目】如图,正五边形的边长为2,连接对角线AD,BE,CE,线段AD分别与BE和CE相交于点M,N,给出下列结论:①∠AME=108°;②![]() ;③MN=
;③MN=![]() ;④
;④![]() .其中正确结论的序号是_____.
.其中正确结论的序号是_____.

【答案】①、②、③
【解析】分析:(1)利用等腰三角形的性质,可以得到∠AME度数,(2)证明 △AEM∽△ADE,可以得到![]() ,(3)利用勾股定理求MN的长度,(4)最后求BE=CE=AD.
,(3)利用勾股定理求MN的长度,(4)最后求BE=CE=AD.
详解:
∵∠BAE=∠AED=108°,
∵AB=AE=DE,
∴∠ABE=∠AEB=∠EAD=36°,
∴∠AME=180°-∠EAM-∠AEM=108°,故①正确;
∵∠AEN=108°-36°=72°,∠ANE=36°+36°=72°,
∴∠AEN=∠ANE,
∴AE=AN,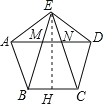
同理DE=DM,
∴AE=DM,
∵∠EAD=∠AEM=∠ADE=36°,
∴△AEM∽△ADE,
∴![]() ,
,
∴AE2=AMAD;
∴AN2=AMAD;故②正确;
∵AE2=AMAD,
∴22=(2-MN)(4-MN),
∴MN=3-![]() ,
,
;故③正确;
在正五边形ABCDE中,
∵BE=CE=AD=1+![]() ,
,
故④错误;
①、②、③正确.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小明用的练习本可以到甲商店购买,也可以到乙商店购买,已知两商店的标价都是每本1元,甲商店的优惠条件是:购买10本以上,从第11本开始按标价的70%卖;乙商店的优惠条件是:每本按标价的80%卖.
(1)小明要买20本时,到哪个商店较省钱?
(2)买多少本时到两个商店付的钱一样?
(3)小明现有32元钱,最多可买多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郴州市正在创建“全国文明城市”,某校拟举办“创文知识”抢答赛,欲购买A、B两种奖品以鼓励抢答者.如果购买A种20件,B种15件,共需380元;如果购买A种15件,B种10件,共需280元.
(1)A、B两种奖品每件各多少元?
(2)现要购买A、B两种奖品共100件,总费用不超过900元,那么A种奖品最多购买多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解八年级男生立定跳远测试情况,随机抽取了部分八年级男生的测试成绩进行统计,根据评分标准,将他们的成绩分为优秀、良好、及格、不及格四个等级,以下是根据调查结果绘制的统计图表的一部分.
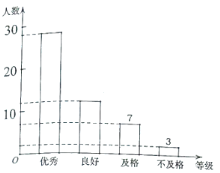
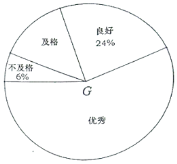
根据以上信息,解答下列问题:
(1)被调查的男生中,成绩等级为不及格的男生人数有__________人,成绩等级为良好的男生人数占被调查男生人数的百分比为__________%;
(2)被调查男生的总数为__________人,条形统计图中优秀的男生人数为__________人;
(3)若该校八年级共有300名男生,根据调查结果,估计该校八年级男生立定跳远测试成绩为良好和优秀的男生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在正方形![]() 中,边长为2的等边三角形
中,边长为2的等边三角形![]() 的顶点
的顶点![]() ,
,![]() 分别在
分别在![]() 和
和![]() 上.下列结论:①
上.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中结论正确的序号是( )
.其中结论正确的序号是( )

A. ①②③B. ①②④C. ①③④D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量保持不变,容器内水量![]() (单位:
(单位:![]() )与时间
)与时间![]() (单位:
(单位:![]() )的部分函数图象如图所示,请结合图象信息解答下列问题:
)的部分函数图象如图所示,请结合图象信息解答下列问题:
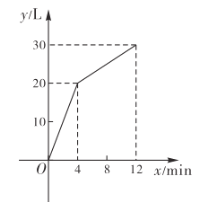
(1)求出水管的出水速度;
(2)求![]() 时容器内的水量;
时容器内的水量;
(3)从关闭进水管起多少分钟时,该容器内的水恰好放完?
查看答案和解析>>
科目:初中数学 来源: 题型:
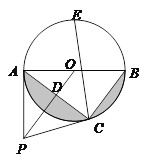
【题目】如图,点P是⊙O 外一点,PA切⊙O于点A,AB是⊙O的直径,连接OP,过点B作BC∥OP交⊙O于点C,连接AC交OP于点D.
(1)求证:PC是⊙O的切线;
(2)若PD=cm,AC=8cm,求图中阴影部分的面积;
(3)在(2)的条件下,若点E是![]() 的中点,连接CE,求CE的长.
的中点,连接CE,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前节能灯在城市已基本普及,某商场计划购进甲、乙两种节能订共1200只,这两种节能灯的进价、售价如下表:
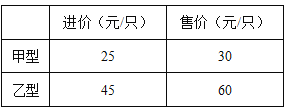
(1)如何进货,进货款恰好为46000元?
(2)为确保乙型节能灯顺利畅销,在(1)的条件下,商家决定对乙型节能灯进行打折出售,且全部售完后,乙型节能灯的利润率为20%,请同乙型节能灯需打几折?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com