
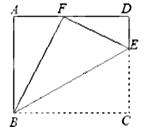
如 图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点
图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点
F落在AD上.
(1)求证:△ABF∽△DFE
(2)若sin∠DFE=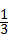 ,求tan∠EBC的值.
,求tan∠EBC的值.
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
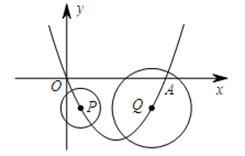
如图,抛物线 y=x2﹣x 与x轴交于O、A两点. 半径为1的动圆⊙P,圆心从O点出发沿抛物线向靠近点A的方向移动; 半径为2的动圆⊙Q,圆心从A点出发沿抛物线向靠近点O的方向移动.两圆同时出发,且移动速度相等, 当运动到P、Q两点重合时同时停止运动.设点P的横坐标为t.若⊙P与⊙Q相离,则t的取值范围是 .
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
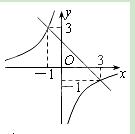
已知一次函数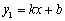 与反比例函数
与反比例函数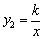 在同
在同 一直角坐标系中的图象如图所示,则当
一直角坐标系中的图象如图所示,则当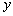 1<
1<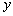 2时,
2时,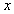 的取值范围
的取值范围 是( )
是( )
A.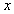 <-1或0<
<-1或0<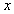 <3 B.
<3 B. -1<
-1<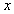 <0或
<0或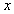 >3
>3
C.-1<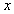 <0 D.
<0 D.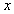 >3
>3
查看答案和解析>>
科目:初中数学 来源: 题型:
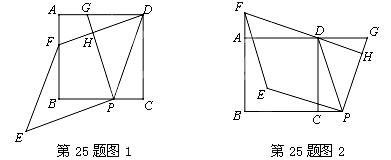
已知,四边形ABCD是正方形,点P在直线BC上,点G在直线AD上(P、G
不与正方形顶点重合,且在CD的同侧),PD=PG,DF⊥PG于点H,交直线AB于点F,
将线段PG绕点P逆时针旋转90°得到线段PE,连结EF.
(1)如图1,当点P与点G分别在线段BC与线段AD上时.
①求证:DG=2PC;
②求证:四边形PEFD是菱形;
(2)如图2,当点P与点G分别在线段BC与线段AD的延长线上时,请猜想四边形PEFD
是怎样的特殊四边形,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,一块直角三角板ABC的斜边AB与量角器的直径重合,点D对应54°,则∠BCD的度数为( )
A. 27° B. 54° C.63° D.36°
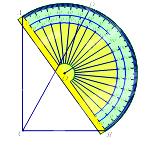
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,线段AC是矩形ABCD的对角线,
(1)请你作出线段AC的垂直平分线,交AC于点O,交AB于点E,交DC于点F(尺规作图,保留作图痕 迹,不写作法)
迹,不写作法)
(2)求证:AE=AF.
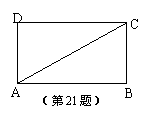
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com