
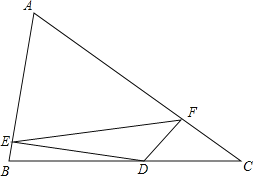
【题目】在△ABC中,AB=5,AC=8,BC=7,点D是BC上一动点,DE⊥AB于E,DF⊥AC于F,线段EF的最小值为_____.
【答案】![]()
【解析】
如图,作CM⊥AB于M,AN⊥BC于N.连接AD,OE,OF.设AM=x,则BM=5﹣x.根据![]() ,可得
,可得![]() ,解得x=4,推出∠EAF=60°,由A,E,D,F四点共圆,推出当⊙O的直径最小时,EF的长最小,根据垂线段最短可知:当AD与AN重合时,AD的值最小,由此即可解决问题.
,解得x=4,推出∠EAF=60°,由A,E,D,F四点共圆,推出当⊙O的直径最小时,EF的长最小,根据垂线段最短可知:当AD与AN重合时,AD的值最小,由此即可解决问题.
解:如图,作CM⊥AB于M,AN⊥BC于N.连接AD,OE,OF.设AM=x,则BM=5﹣x.

∵CM2=AC2﹣AM2=BC2﹣BM2,
∴82﹣x2=72﹣(5﹣x)2,
解得x=4,
∴AM=4,AC=2AM,
∴∠ACM=30°,∠CAM=60°,CM=![]() AM=4
AM=4![]() ,
,
∵S△ABC=![]() BCAN=
BCAN=![]() ABCM,
ABCM,
∴AN=![]() ,
,
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°,
∴A,E,D,F四点共圆,
∴当⊙O的直径最小时,EF的长最小,
根据垂线段最短可知:当AD与AN重合时,AD的值最小,AD的最小值为![]() ,
,
此时OE=OF=![]() ,EF=2OEcos30°=
,EF=2OEcos30°=![]() ,
,
∴EF的最小值为![]() ,
,
故答案为![]() .
.


 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,点D、E分别在边
,点D、E分别在边![]() 上,连接DE,且
上,连接DE,且![]() .
.
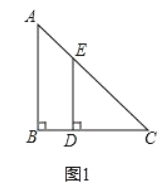

(1)问题发现:若![]() ,则
,则![]() ______________________.
______________________.
(2)拓展探究:若![]() ,将
,将![]() 饶点C按逆时针旋转
饶点C按逆时针旋转![]() 度
度![]() ,图2是旋转过程中的某一位置,在此过程中
,图2是旋转过程中的某一位置,在此过程中![]() 的大小有无变化?如果不变,请求出
的大小有无变化?如果不变,请求出![]() 的值,如果变化,请说明理由;
的值,如果变化,请说明理由;
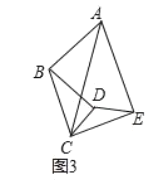
(3)问题解决:若![]() ,将
,将![]() 旋转到如图3所示的位置时,则
旋转到如图3所示的位置时,则![]() 的值为______________.(用含
的值为______________.(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AC平分∠BAD,延长DC交AB的延长线于点E .
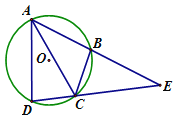
(1)若∠ADC=86°,求∠CBE的度数;
(2)若AC=EC,求证:AD=BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k≠0)与反比例函数y=![]() (a≠0)的图象在第一象限交于A、B两点,A点的坐标为(m,4),B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C.若OC=CA,
(a≠0)的图象在第一象限交于A、B两点,A点的坐标为(m,4),B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C.若OC=CA,
(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积;
(3)在直线BD上是否存在一点E,使得△AOE是直角三角形,求出所有可能的E点坐标.
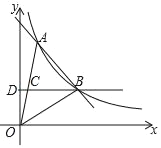
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某产品每件成本为20元,经过市场调研发现,这种产品在未来20天内的日销售量![]() (单位:件)是关于时间
(单位:件)是关于时间![]() (单位:天)的一次函数,调研所获的部分数据如下表:
(单位:天)的一次函数,调研所获的部分数据如下表:
时间 | 1 | 3 | 10 | 20 |
日销售量 | 98 | 94 | 80 | 60 |
这20天中,该产品每天的价格![]() (单位:元/件)与时间
(单位:元/件)与时间![]() 的函数关系式为:
的函数关系式为:![]() (
(![]() 为整数),根据以上提供的条件解决下列问题:
为整数),根据以上提供的条件解决下列问题:
(1)直接写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)这20天中哪一天的日销售利润最大,最大的销售利润是多少?
(3)在实际销售的20天中,每销售一件商品就捐赠![]() 元(
元(![]() )给希望工程,通过销售记录发现,这20天中,每天扣除捐赠后的日销利润随时间
)给希望工程,通过销售记录发现,这20天中,每天扣除捐赠后的日销利润随时间![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线C1:y=ax2+bx+c经过点A(-1,0)、B(3,0)、C(0,-3).
(1)求抛物线C1的解析式;
(2)将抛物线C1向左平移几个单位长度,可使所得的抛物线C2经过坐标原点,并求出C2的解析式;
(3)把抛物线C1绕点A(-1,O)旋转180°,写出所得抛物线C3顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,点D在AC边上,以AD为直径作⊙O交BD的延长线于点E,CE=BC.
(1)求证:CE是⊙O的切线;
(2)若CD=2,BD=2![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在等腰三角形中,底边与腰的比叫做顶角的正对,顶角A的正对记作sadA,即sadA=底边:腰.如图,在△ABC中,AB=AC,∠A=4∠B.则cosBsadA=( )

A.1B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com